Aerospace Micro-Lesson #27
In This Section
How High is it?
Asking how high something is seems to be a very simple question to answer. If you think about it closely, though, details emerge that are anything but simple. Exactly which direction is “up”? Exactly what level is the zero point? How does the zero point in one place relate to the zero point elsewhere? How do you measure the height of something that you cannot reach yourself, or from which you cannot drop a measuring tape down to the zero level?
GRADES K–2
There are several different ways to figure out how high something is. If it is short enough for you to reach it, you can hang a measuring tape from it and measure it that way.
Another way to measure the height of something is to set up something shorter next to it, something whose height you know. If they are outside in the sunlight, you can see how long the shadows are that they cast. With some elementary arithmetic (which you will learn in a couple of grades) you can use the lengths of the shadows to figure out how tall the object is.
A third method is called the “artist’s method.” You stand back from the object you are measuring and hold up a pencil at arm’s length in front of you. (If you are an artist, you hold up a paintbrush.) You move your thumb along the pencil until the point of the pencil lines up with the top of the object and your thumb on the pencil lines up with the bottom of the object. Then you turn the pencil so that it is horizontal and your thumb still lines up with the bottom of the object. Have a friend stand next to the object, moving away from it (but keeping the same distance from you) until the point of the pencil lines up with your friend. The distance from your friend to the object is the same as the height of the object. You can coordinate with an art teacher in presenting this method.
GRADES 3–5
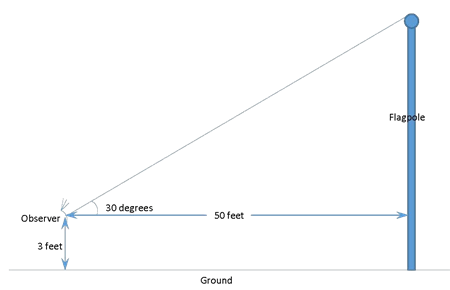
One way to measure the height of something is to stand some distance from it and measure the angle from the horizontal to the top. Then you can draw a scale diagram, measure the height of the object in the diagram, and use a ratio to calculate the true height of the object. This diagram shows the sort of figuring that one does if one measures an angle of thirty degrees to the top of a flagpole fifty feet away:
In the diagram, the diagonal line measures four inches horizontally and two and a third inches vertically. One can use a ratio to calculate the height of the flagpole in real life:
Multiplying the ratio out gives
The “3 feet” on the left is the height of the observer’s eyeball above the ground. One needs to add it to the “Height above observer” to get 31.8 feet as the height of the flagpole.
GRADES 6–8
The basic shape of the Earth is an ellipsoid: a cross-section through the Equator (or a line of latitude) is a circle and a cross-section through a line of longitude is an ellipse. The elliptical shape results from the rotation of the Earth and is changed from a circle by about 0.3 percent, or one part in three hundred. This is not noticeable to the unaided eye. (The planets Jupiter and especially Saturn, in contrast, rotate more than twice as quickly as the Earth and have visibly elliptical shapes.)
The ellipsoidal shape of the earth complicates the question of defining a zero altitude. If a person starts at zero altitude on the Equator and goes to the North Pole, moving neither up nor down in altitude, one moves about 13 miles closer to the center of the Earth. (For comparison, Mount Everest is less than six miles high.) Zero altitude cannot be defined as being a constant distance from the Earth’s center, then. Instead, zero altitude is often considered as the Mean Sea Level. Mean Sea Level is the level of the oceans when the effects of tides, currents, winds, and waves are removed. It can never be measured directly but must be calculated by averaging (hence the term “mean”) many thousands of observations of individual sea levels.
Because the Earth is not a perfect sphere, the direction of “up” must also be considered carefully. This is not so much of an issue in determining how high something is, but it is still an issue. “Up” is the direction perpendicular to the surface of the Earth. This is not the same thing as the direction directly away from the center of the Earth unless one is at the Equator or one of the poles.
GRADES 9–12
The ellipticity of the Earth is not the only complication in defining zero altitude. Mountains have mass; their mass exerts a gravitational force; this gravitational force distorts which direction is “up.” If one moves westward (along a line of constant latitude, supposedly circular in shape) in Colorado towards the Rocky Mountains, for example, even if one is not moving sensibly “up” or “down” one is getting farther from the center of the Earth. In the other direction, a trench in the ocean is filled with water which is less dense than the rock that is underneath the ocean around it. Because the water is less dense, its gravitational force is less, and the rock beside the trench pulls the water away from the trench itself. The sea level above an oceanic trench can be as much as 65 feet lower than the sea level above the ocean of average depth.
There is an entire science called “geodesy” which is devoted to measuring and calculating the shape of the Earth. Geodetic scientists have defined the shape of the Earth, which is called the “geoid,” using sines and cosines of the latitude and longitude to a precision of about 30 miles, or half a degree of latitude (and of longitude at the Equator). This definition requires a total of 130,317 coefficients in their equation that defines the shape of the Earth; this equation gives the distance of the geoid above the average ellipsoidal shape of the Earth at any latitude and longitude. As such, there are two ways to express the altitude of any point on the Earth’s surface. One can give a number as the “height above the ellipsoid” (abbreviated “HAE”), which gives the distance of the point above the Earth’s ellipsoidal shape. More commonly, one can give the height above Mean Sea Level (abbreviated “MSL”), which is the same as the height above the geoid.
When something is above or below the surface of the Earth, there is a third way to express its altitude. There are the HAE and MSL altitudes; in addition, there is the object’s altitude above ground level, abbreviated “AGL.” When one is flying an airplane it is important to keep the altitude AGL greater than zero.
If one asks how high a mountain is, one must define one’s terms carefully. The highest mountain in the world is Mount Everest, whose altitude is 29,029 feet (8,848 meters) above Mean Sea Level. (It should be noted that this figure is not as accurate as it looks, in part because of defining “Mean Sea Level” at the Himalayan Plateau.) The tallest mountain in the world is Mauna Kea in Hawaii, which extends vertically 33,465 feet (10,200 meters) from its base on the floor of the Pacific Ocean to its peak on the Big Island of Hawaii. The point on the surface of the Earth that is farthest from its center is the peak of Mount Chimborazo in Ecuador, even though its height is “only” 20,703 feet (6,310 meters) above Mean Sea Level.
There are other types of altitude that motivated students can look up. “Pressure altitude” relates to atmospheric pressure and varies with the weather. “Geopotential altitude” adjusts for the lessening of the Earth’s gravity as the altitude increases. The question of defining a zero point on the moon or Mars, where there is no sea and therefore no Mean Sea Level, opens an entirely different can of worms. On Mars, the zero altitude was specified arbitrarily as the altitude at which the atmospheric pressure is 610.5 Pascals, which is the pressure of the triple point of water.
Sixty Years Ago in the Space Race:
November 1956: The Americans launched twelve sounding rockets, eleven successfully, to study the upper atmosphere and to test re-entry vehicle technology. A sounding rocket simply goes up and comes down; it does not orbit the Earth or even necessarily go into space.