Aerospace Micro-Lesson #9
In This Section
Transit of Mercury
On the morning of Monday, November 11, 2019, the planet Mercury will pass in front of the sun. This is the first time this has happened since 2016; the next time it happens will be on November 13, 2032; the next time it will be visible from the United States will be 2049. Teachers are strongly encouraged to contact a local astronomical society or university to arrange a visit so that the students can look through a telescope with a good solar filter to view the transit. The transit begins at 7:36 AM Eastern Daylight Time (6:36 AM Central, 5:36 AM Mountain, and 4:36 AM Pacific) and ends at 1:04 PM Eastern (12:04 PM Central, 11:04 AM Mountain, 10:04 AM Pacific).
Next Generation Science Standards (NGSS):- Discipline: Space Systems
- Crosscutting Concept: Patterns and Cycles
- Science & Engineering Practice: Analyzing and Interpreting Data
GRADES K-2
1-ESS1-1. Use observations of the sun, moon, and stars to describe patterns that can be predicted.
The planet Mercury goes around the Sun, just as the Earth does, but Mercury is closer to the Sun and goes around more quickly. The distance from the Sun to Mercury is just less than half the distance from the Sun to the Earth. It takes Mercury 88 days to go around the Sun once; thus it goes around the Sun about four times in the amount of time it takes the Earth to go around the Sun once.
You can illustrate the arrangement with a lamp or light bulb representing the Sun, a globe or a ball representing the Earth, and a ball representing Mercury. (The diameter of Mercury is just less than half the diameter of the Earth.) Have one person hold the globe several feet from the light bulb while another person holds the ball representing Mercury closer to the Sun. Then the person holding Mercury can move it around the Sun one full revolution while the person holding the Earth goes one quarter of the way around.
The image below is from the 2016 transit, showing the planet’s progress across the face of the sun. The map of the earth shows which areas will have a view of Mercury’s progress during the 2019 transit. For more information about Mercury, visit NASA’s SpacePlace.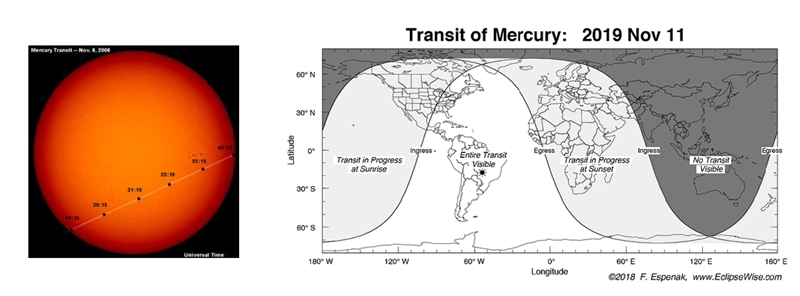
GRADES 3-5
If it is not possible to arrange for the students to view the transit “live” through a telescope with a solar filter (or, for example, if the sky is overcast), there will be pictures available on the Internet. It is much better to get out and actually watch the event oneself, though; there is a certain element of “coolness” and involvement that comes from seeing the event itself that one does not get from looking at pictures of the event. Even if the pictures are more spectacular than the view of the event itself, they suffer from a level of detachment. The realization that “photons that left the Sun eight minutes ago are now hitting my eyeball” is an element that pictures will never duplicate. The reason that transits of Mercury are so rare (and transits of Venus are even rarer) is because the orbits of the planets are tilted with respect to one another. In the demonstration in the Grades K-2 lesson, the student holding the ball representing Mercury can move it in a plane that is tilted. Most of the time, the ball will not pass directly between the globe and the light bulb; it will pass either above or below the point directly between. In the same way, the inner planets usually pass either north or south of the point directly between the Earth and the Sun.
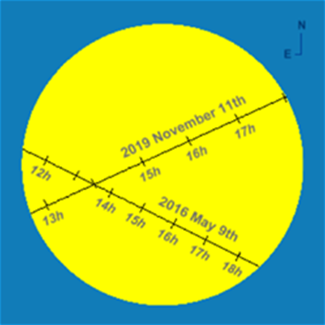
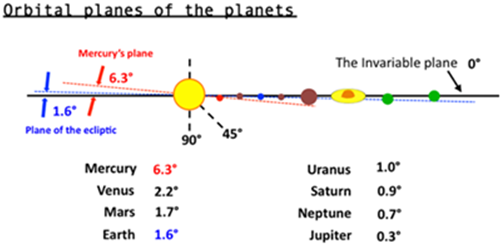
The diagram on the left shows the difference in angles between the 2016 transit and this year’s occurrence. This year’s transit will be at a different angle from our viewpoint, based on the different orbital planes of the planets (as seen on the right).
 |
 |
GRADES 6-8
If the students get outside to look at the transit through a telescope with a typical solar filter, they will see a white circle in the eyepiece of the telescope. This white circle is the Sun. Somewhere on that white circle there will be a small black dot with sharp edges; this is the planet Mercury. The position of the planet on the Sun will vary depending on the time at which one is looking at the transit. Which way is north on the Sun relative to which way is “up” on the view in the eyepiece also varies depending on the optics of the telescope, the position of the Sun in the sky, and other factors.
In addition to the small dot with sharp edges, there are also very likely to be other dark regions on the white circle. These dark regions are sunspots. They vary in size and shape; many of the larger ones will have lighter edges. Some sunspots are larger than the Earth in diameter. You can find a daily view of where the sunspots are on the sun here (look for the “Daily Sun” on the left-hand side of the page).
The Wikipedia article on Transits of Mercury has some interesting historical data and other information.
GRADES 9-12
Astronomers in centuries past used the transits of the inner planets as a way to measure the size of the Solar System. While they could measure the angles between things very accurately, it was extremely difficult to measure distances. Astronomers therefore defined the “Astronomical Unit” as the mean distance from the Earth to the Sun and calculated other distances in the Solar System in terms of Astronomical Units, abbreviated as “AU.”
With Kepler’s calculation of the orbits of the planets, it became possible to predict when Mercury and Venus would pass in front of the Sun. Astronomers quickly realized that this would allow them to measure the size of the Astronomical Unit. Consider the following geometry:
A planet (Mercury or Venus) is a distance “DP” from the Sun; the Earth is a distance “DE” from the Sun. The planet is moving at a speed of “VP” while the Earth is moving at a speed of “VE”. These speeds can be calculated by taking the circumference of the orbit and dividing by the number of seconds in each planet’s year. Using geometry, we can calculate the distances “DP” and “DE” from the planet’s apparent speed during a transit.
Consider the triangle with the base “DP”, the lower left vertex at the Sun, and the right-hand side with a height “VP t”, which we can think of as distance the planet travels in a short time “t” (one second). Consider then the similar triangle with base “DE”. In one second, the height “H” of the right-hand side will be the ratio from the other numbers:
.png?sfvrsn=c29a054e_3)
In that one second “t”, the Earth has traveled a distance of “VE t” in its orbit, which we need to subtract from “H” to get the distance that the “shadow” of the planet travels across the earth’s surface. (There needs also to be some correction for the fact that the Earth’s surface is a sphere, not flat and facing the Sun.)
For Earth, “DE” is 1.000 AU, one orbit takes 365.2 days (31.56×106 seconds), and “VE” is 0.199×10-6 AU per second. For Mercury, “DP” is 0.387 AU, one orbit takes 88.0 days (7.60E6 seconds), and “VP” is 0.320×10-6 AU per second. Thus the rate at which Mercury’s “shadow” sweeps across the earth is 0.627×10-6 AU per second. If two observatories, one of them five thousand miles west of the other (5,400 miles after correcting for the roundness of the earth), observe the transit of Mercury start 86 seconds apart (which is our value for “t”), we can calculate that one AU equals about 93×106 miles. (The true value is 92.9565×106 miles.)
Sixty Years Ago in the Space Race: