Aerospace Micro-Lesson #31
In This Section
Ride a Sounding Rocket
A “sounding rocket” is one which goes up into space and comes directly back down rather than putting a satellite into orbit or launching something farther into space. NASA launched a sounding rocket on March 23, 2011 from southern New Mexico. They put together a four-and-a-half-minute video from two cameras mounted on the rocket. You can see the video here. It shows all the stages of the trajectory, from launch to burnout, coasting through space, re-entry, landing, and finally retrieval. (Stages in which nothing much is happening are fast-forwarded.)
Next Generation Science Standards (NGSS):
- Discipline: Physical Science
- Crosscutting Concept: Structure and Function
- Science & Engineering Practice: Developing and Using Models
Common Core State Standards (CCSS):
- Measurement & Data
- Ratios & Proportional Relationships
GRADES K–2
NGSS: Space Systems: Patterns and Cycles: Use observations of the sun, moon, and stars to describe patterns that can be predicted.
A short geography lesson would be to find southern New Mexico on the globe. The launch site was at latitude and longitude “32.4181, -106.3199” (
you can find it on Google Maps). If you freeze the video around 26 seconds (just before launch), you can see the building at “
32.4179, -106.3203”. The building looks sideways in the video because the camera on the rocket was mounted sideways. The Google Maps view shows the shadow of the mast on the east side of the building; in the video it is on the front of the building. If you freeze the
video at 31 seconds (just after launch—this is trickier because the rocket is ascending quickly) you can also see the other buildings behind, meaning to the west-south-west, of that building. The “building” on Google Maps between the launch site and the building with the
mast appears to be movable; in the video at 31 seconds you can see it much closer to the red-and-white mast than it appears on Google Maps.
The path of the rocket went straight up from the launch site, peaked at 178 miles high, and came more-or-less straight back down. The greatest height, 178 miles, is about one fortieth to one fiftieth of the earth’s diameter; thus on a globe 15 inches across, the trajectory would come up about a third of an inch from the surface.
The “height of the atmosphere” is set at about 62 miles high, or about one third of the height of the trajectory. Thus on a fifteen-inch globe, the atmosphere would be a layer all around it about an eighth of an inch thick. There isn’t a real boundary between the atmosphere and outer space; the air simply gets thinner and thinner the higher one goes. The boundary at 62 miles is simply a line drawn by scientists and engineers. The thinness of the eighth-of-an-inch layer around the globe is not a reflection of how thin the atmosphere is; it is more a reflection of just how big the earth is.
GRADES 3–5
NGSS: Motion and Stability: Forces and Interactions: Support an argument that the gravitational force exerted by Earth on objects is directed down.
As the rocket is going up, it spins rapidly. This helps it keep pointing forward and going in a straight line. There are two principles in play here. The first is that when a flying object spins, any asymmetries that would cause it to move sideways spin around with the object and cancel each other out. If something is sticking out to the left that would cause the rocket to turn to the left, half a turn later it is sticking out on the right and causing the rocket to turn to the right. The overall effect is that the rocket moves in the forward direction.
The second effect is the gyroscopic effect that a spinning body tends to keep pointing in the same direction. You can illustrate this in the classroom by bringing in a top. If the top is not spinning and you set it on its tip, it will fall over immediately. If it is spinning, though, it will not fall over.
You may want to calculate how long the rocket was in flight. The video has a few segments which are played back faster than normal. I measured the following times from the video:
0:30 into the video – Launch
2:28 – start of 30x speed (meaning one second in the video is 30 seconds of rocket flight)
2:39 – normal speed
3:05 – start of 25x speed
3:19 – normal speed
3:43 - landing
We take all the differences between these video times and find that the rocket was flying for one minute 58 seconds (or 118 seconds) of normal video speed, 11 seconds of 30x speed, 26 seconds of normal speed, 14 seconds of 25x speed, and 24 seconds of normal speed. To get the flight time we multiply our sped-up intervals by the speeds and then add all the times together:
Thus the rocket was in flight for 848 seconds, or just over fourteen minutes.
After the landing, the video accelerates to 650x speed at 3:48 and comes back to normal speed at 3:57. Those nine seconds of video time represent 5850 seconds of time that the rocket was on the ground, or just over an hour and a half. You can see the direction of the shadows caused by the sun moving during that hour and a half.
GRADES 6–8
NGSS: Motion and Stability: Forces and Interactions: Construct and present arguments using evidence to support the claim that gravitational interactions are attractive and depend on the masses of interacting objects.
CCSS: Math: Ratios & Proportional Relationships: Use ratio reasoning to convert measurement units; manipulate and transform units appropriately when multiplying or dividing quantities.
If you look at the launch site on Google Maps, you can tell from the directions of the shadows that the satellite pictures were taken fairly early in the morning. (Every mast and telephone pole acts like the gnomon of a sundial; you can measure the angle with a protractor, divide by fifteen degrees per hour, and get that the picture was taken around 7:30 AM. Unfortunately the seasonal variation of where the sun rises makes early morning and late afternoon determinations quite inaccurate.) If you freeze the video at 31 seconds, you see that the shadow of the tall red-and-white mast falls across the small almost-square building just west of the building with the mast. You can therefore conclude that the launch took place around 9:30 AM. Using the time measurements and calculations given in the Grades 3-5 lesson, the rocket was retrieved a little before noon. Again, these are very rough observations and the results are probably only accurate to within an hour or so.
Freezing the video during ascent is a little tricky because of the rocket’s spin but can show some local geographical features. At 0:33, just as the spin is beginning, one can see the complex of roads between “ 32.4168, -106.3219” and “ 32.4123, -106.3219”. I think the light-colored area visible around 0:46 is the patch at “ 32.47, -106.38”. Ten seconds later, at 0:56, the glaring white of the White Sands National Monument comes into view; a few seconds later (around 1:00) with a few tries one can freeze the video so that it is in the frame and one can distinguish some rough outlines of the shapes of its southern edge. The view gets more panoramic over the next minute or so, and is much easier to see when the spin stops around 1:50. The dark area to the east (preceding) White Sands National Monument is the Lincoln National Forest; to the west of White Sands you can see the San Andres National Wildlife Refuge. To the west and south of that you can see the Rio Grande as a darker winding line through the lighter-colored countryside. At 1:51 you can see a twisting white line that is a salt flats about 100 miles southeast of the launch site, next to the Guadeloupe Mountains in Texas.
I’ve not been able to find the rocket’s specific landing point. Because it went more-or-less straight up to a height of 178 miles and came straight back down, the landing site must be within a few tens of miles of the launch site and may be much, much closer. The image is much degraded because of the heat, not just from the sun but also from re-entry. I think, but I am not sure, that the linear feature in the picture around 3:22 is Highway 70 south of White Sands National Monument. You can see the south edge of the white sands to the left in the picture. With a little more effort one may be able to figure out the exact landing spot but I have not put forth that effort. The dark feature that appears at 3:29 is the shadow of the cruciform parachute; you can see the shadow of the rocket underneath it at 3:36.
GRADES 9–12
NGSS: Motion and Stability: Forces and Interactions: Analyze data to support the claim that Newton’s second law of motion describes the mathematical relationship among the net force on a macroscopic object, its mass, and its acceleration.
The rocket passed the Von Karman Line, which marks the “boundary” between the atmosphere and outer space, at 1:34 in the video. By this time it is coasting; without atmospheric drag on it, the only force acting on it is gravity. While the gravitational acceleration decreases as one gets farther from the center of the earth, the difference is about five percent and our measurements are rougher than that. We therefore use a constant gravitational acceleration of 32.174 ft/sec2 (9.81 m/s2).
It is a little hard to see, but the rocket reaches its apogee (the highest point in the trajectory) at 2:33 in the video. The 30x speedup started five seconds earlier, at 2:28. The time that the rocket took to go from 62 miles to 178 miles is ( 2:28 – 1:34 ) x 1 + ( 2:33 – 2:28 ) x 30 = 204 seconds. (Because of the 30x speedup, this number could easily be off by 15 or 30 seconds.) We can use the constant acceleration formula
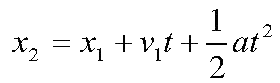
to check our numbers. In this formula, “x2” is the altitude at one point in our trajectory; “x1” is the altitude at another point in our trajectory. While “x1” usually is earlier than “x2”, it does not have to be; in our case we will choose “x1” to be apogee (178 miles or 940,000 feet or 286,000 meters) and “x2” to be the top of the atmosphere (62 miles or 327,000 feet or 100,000 meters). The “v1” is the vertical velocity at our “x1” point; at apogee, the vertical velocity is zero. The “t” is the time between the two events and “a” is the acceleration, in our case the gravity. If we specify our positive direction as going up, “a” is a negative number.
Solving the constant acceleration formula for “t” (and using the fact that “v1” is zero) gives
Our altitude “x2” is less than “x1” so the numerator of the fraction is negative; the acceleration is also negative, so we will be taking the square root of a positive number. Thus the mathematics works out as the physics works out. Substituting our values in gives a time of 195 seconds. This is within ten seconds of our measured time of 204 seconds. (Incidentally, if you make a detailed calculation of the acceleration due to gravity and use its actual value at 32.4 degrees latitude, your resulting time will be almost 200 seconds, reducing the discrepancy between calculated and measured time further.)
On the way down, the rocket passes the 62-mile mark at 3:09 in the video. This is during the 25x speedup. From the times recorded in the Grades 3-5 lesson, our mission time from apogee down to the 62-mile altitude is ( 2:39 – 2:33 ) x 30 + ( 3:05 – 2:39 ) x 1 + ( 3:09 – 3:05 ) x 25 = 306 seconds. From our altitude and acceleration calculations, we should get a time of about 195 seconds because it takes as much time to come back down as it did to go up. This discrepancy of over 100 seconds is well outside the uncertainty of our calculation and shows that something is wrong with the data. It is entirely possible—and well within the purposes of the video, which was never intended to be subjected to detailed mathematical analysis such as this—that the start or stop times of one of the time speedup intervals was off of the value that I measured for it by three seconds.
There are more videos from sounding rocket missions on You-Tube:
https://www.youtube.com/watch?v=GLhaNd_H5bM
https://www.youtube.com/watch?v=OdKw38BaP5s
Unfortunately they are for different missions and so while they are good for overall insight into what is happening, they do not help in figuring out the specifics of this mission.
Sixty Years Ago in the Space Race:
January 25, 1957: The first test flight of the American Thor intermediate range rocket failed when it exploded after rising six inches from the launch pad. Contaminated liquid oxygen was blamed for causing a valve to stick.