Aerospace Micro-Lesson #32

Earth's Weather

There is a web site that contains an interactive visualization of the earth's weather.  It shows the global wind patterns, temperatures, atmospheric water content, and many other things, from ground level up through various altitudes in the atmosphere.  You can zoom in and out and rotate the globe by clicking and dragging the mouse and by rotating the mouse wheel.  You can ask for point data with a left mouse-button click.  If you click on the word "earth" in the lower left-hand corner of the screen a menu comes up which allows you to specify what you want plotted.  (Clicking on the word "earth" again makes the menu go away.)  The data are updated every three hours.

Next Generation Science Standards (NGSS):

• Discipline: Earth and Space Sciences
• Crosscutting Concept: Patterns.
• Science & Engineering Practice: Analyzing and Interpreting Data.

Common Core State Standards (CCSS):

• Functions: Linear, Quadratic, and Exponential Models.

GRADES K–2

NGSS: Earth's Systems: Use and share observations of local weather conditions to describe patterns over time.

There is a video on You-Tube titled “ Meteorologist Explains Weather Maps.”  In this video, Mr. Davidson (the meteorologist) shows what some of the symbols used in weather maps mean and explains concepts like fronts and pressure systems.  At the end of the video, he shares the week's forecast for a particular area.  Teachers can use it along with their daily calendar time when they talk about the daily weather, and then have the students talk about places they have seen weather maps—newspapers, local TV, The Weather Channel, for example—and why people need weather maps.

Kindergarten students can discuss the weather shown in the forecast.  How many cloudy days do you see?  How many sunny days?  First grade students might talk about the concept of predictions.  The meteorologist predicts the weather from making observations, looking at clouds, wind, and what is happening in areas nearby that might move into their own area.  Second graders might try to identify in what season the video was made.  Look at the daytime and nighttime temperatures and the types of precipitation that appear on the weather map.

For those wishing for more information about various types of weather, the National Weather Service has a two-part video explaining weather for kids (how weather forms, different types of weather, what a meteorologist does, even a water cycle rap song): 

For background information to help teachers discuss the subject with their students, there is a website that caters to kids interested in/studying weather.  It provides explanations for many of the symbols used on weather maps and what the various terms mean.

GRADES 3–5

NGSS: Earth's Systems: Obtain and combine information to describe climates in different regions of the world.

A good exercise would be to get a globe and compare the continents and islands on the globe with their outlines on the global weather map.  One can then zoom in on one's own location on the globe and see which direction the wind is blowing.  (For the younger students, you may want to confine yourself to the surface wind pattern.)  Compare this with what you see yourself at your school.  Do not be surprised if what you see does not match what the weather map shows, especially on a calm day; local effects can override the larger-scale patterns shown on the weather map.

You can also watch the “Meteorologist Explains Weather Maps” video and then look at the day’s weather map.  Comparing the features on the weather map to the wind patterns on the global map would be instructive.

During hurricane season, or if there is a major storm somewhere, it is very instructive to find the location of the storm and see its wind patterns.  It is also instructive to compare the different temperatures and wind patterns at different altitudes, to see how high different weather patterns (such has hurricanes or typhoons) extend.  Another possible exercise might be to find the jet stream.

GRADES 6–8

NGSS: Earth's Systems: Collect data to provide evidence for how the motions and complex interactions of air masses results in changes in weather conditions.

The altitudes given in the weather map are “pressure altitudes.”  A pressure altitude of a certain value is the altitude at which the atmospheric pressure has that value.  The pressure altitudes in the visualization are given in "hectoPascals," or "hundreds of Pascals."  One Pascal of pressure is one Newton per square meter; another way of saying this is that a pressure of one Pascal exerted over an area of one meter by one meter pushes with a force of one Newton.  Atmospheric pressure at sea level has a pressure of 1,013 hPa, which is equal to the familiar 14.7 psi (pounds per square inch).

The given altitudes are as follows:

• Sfc – surface, nominally sea level
• 1000 hPa – about 370 feet, or 110 meters above sea level
• 850 hPa  – about 5,000 feet, or 1,500 meters above sea level
• 700 hPa  – about 10,500 feet, or 3,200 meters above sea level
• 500 hPa  – about 20,000 feet, or 6,000 meters above sea level (Mount Everest is about 29,000 feet high)
• 250 hPa  – about 40,000 feet, or 12,000 meters above sea level
• 70 hPa   – about 75,000 feet, or 23,000 meters above sea level
• 10 hPa   – about 130,500 feet, or 40,000 meters above sea level

If you plot the temperatures at different altitudes, you will see that as you go up in height the air gets colder.

The air pressure at any given position in the earth's atmosphere is caused by the weight of all the air above that point pressing down on it.  One can visualize the air pressure by telling the kids to "hold out your hand.  Imagine a square inch on the palm of your hand; now imagine a column of air one square inch in area going from your hand all the way up through the atmosphere into space.  All the air in that column weighs 14.7 pounds."  They don't feel the weight because for each square inch on the palms of their hands there is a square inch on the backs of their hands on which the air is pressing upwards with a force of 14.7 pounds.  Please note that at higher altitudes, such as those in Colorado, the air pressure is somewhat less than 14.7 pounds per square inch because there is less air pressing down from above.

GRADES 9–12

NGSS: Earth's Systems: Use a model to describe how variations in the flow of energy into and out of Earth's systems result in changes in climate.

CCSS: Functions: Linear, Quadratic, and Exponential Models: Distinguish between situations that can be modeled with linear functions and with exponential functions.

In addition to hurricanes, typhoons, and other tropical cyclones, students may want to look at regular warm and cold fronts on a current weather map and compare them to what the animation shows.  During the winter in either hemisphere, one can see a rather strong (and cold) polar vortex circulating at high altitude above the wintering pole.

The animation also shows sea surface data, including waves and currents.  One can find the Gulf Stream as well as several other ocean currents.  These currents are not simple, smoothly-flowing bodies of water; there are eddies that pinch off of their edges and meander away.

Advanced students with some knowledge of calculus may want to derive how to calculate the atmospheric pressure as a function of altitude with an eye to converting “pressure altitude” to geometric altitude.  One can draw a thin horizontal box at some altitude “z” and calculate the forces on the air in the box.  If the horizontal cross-section area of the box is “A” and the (vertical) thickness of the box is “D”, then the mass of the air in the box is “r A D", where “r” is the density of the air.  The force of gravity “F_g” acting on the air is given by the formula (with a minus sign indicating that it is pulling down)

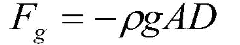
In this equation, “g” is the gravitational acceleration.  It actually varies slowly with altitude, but we will neglect that variation for lower altitudes.  We will refer to the pressure at the altitude “z” at the bottom of the box as the function “P(z)” and the pressure at the altitude “z + D” at the top of the box as “P(z+D)”.  Because the pressure is the force per unit area, the force “F_PB” that the air exerts pushing up on the bottom of the box is given by the formula:

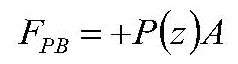
Similarly, the force “F_PT” of the air pushing down on the top of the box is given by the formula:

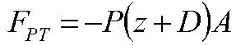
Since our block of air is sitting still, the forces on it must balance:

Substituting in gives:

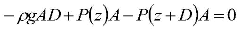
The “A” in each term cancels out, meaning that our derivation does not depend on the horizontal size of the box.  This is an excellent common-sense check.

We now need to use the perfect gas equation of state.  This is a generalization of Boyle’s Law (that the pressure on a given amount of gas, multiplied by the volume of that amount of gas, at constant temperature, is a constant) and Charles’ Law (that the volume of a given amount of gas, divided by the temperature of that amount of gas, at constant pressure, is a constant).  It is given by the formula:

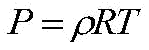
where “R” is our “gas constant.”  We solve for the density “p” and substitute this into our balance of forces equation:

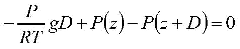
Astute readers will note that our “P” in the first term does not have an argument.  Strictly speaking, we took our density at the center of our box and so our pressure should be taken at that altitude (which would be “z+ (1/2) D”) as well.  In fact, when we specify “D” to be small enough, we can specify that the pressure in the first term can be taken from anywhere inside the box.

Now the knowledge of calculus comes in.  The definition of the derivative of a function at a point “h” is the slope of the curve of the function:

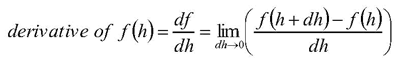
In this formula, “lim” means “find the limit as a small quantity called ‘dh’ approaches zero.”  Our balance of forces equation has for its second and third terms a function (the pressure “P”) evaluated at two points (“z” and “z+D”) that are very close together.  We rearrange the terms in our balance of forces equation to show this more clearly:

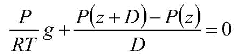
We match this equation with the equation that defines the derivative of a function.  Our pressure “P” is our function “f”; our altitude “z” is our variable “h”; and our box thickness “D” is our small change “dh” to our variable.  If we let our box thickness “D” get arbitrarily small (and this is why it does not matter where in the box we take our pressure in the first term of the force balance equation), our force balance equation becomes:

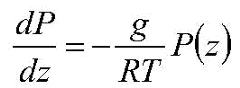
If we wish to be pedantic, we should specify that “D” becomes arbitrarily small but stays large enough that the size and spacing of the molecules in the air does not become an issue.

Now let us consider the exponential function:

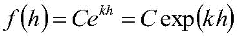
In this equation, “C” and “k” are arbitrary constants. If we find the derivative of this function, our formula gives the following:

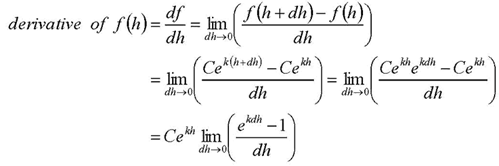
The next step is to evaluate the limit.  If we let “dh” go to zero, then our constant “k” multiplied by “dh” will also go to zero.  We multiply and divide our limit by “k”:

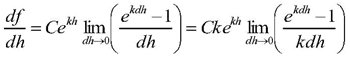
This limit is the “rise over the run” of the exponential function at “h = 0”, which is one.  Our formula for the derivative is therefore:

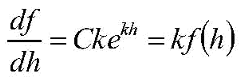
Now we look at the last version of our force balance equation. Our constant “k” is “–g/RT” and our function “f(h)” is “P(z)”.  Our other constant “C” is the pressure at zero altitude, “P₀”, which has a value of 1,013.25 hPa.  We find that our pressure as a function of altitude is given by an exponential function:

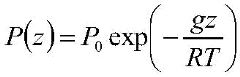
It should be noted that this derivation assumes that the temperature does not change with altitude; while this is not exactly true, it is close enough for rough calculations.  I suggest that an “average” sort of temperature be used, such as 250 K; the temperature in theatmosphere below about 25 kilometers (82,000 feet) ranges between 288 K and 216 K.  Gravity at sea level is 9.81 m/s².  The gas constant “R” for air is 287 m²/s²-K.  The students can now calculate the pressure altitude in terms of the geometric altitude. Depending on the choice for the temperature, they should get results that are within about ten percent of the given values.

Sixty Years Ago in the Space Race:

February 13, 1957:  The first Australian Skylark rocket was launched at Woomera, Australia to a height of 50,000 feet and landed 20 miles downrange.