Aerospace Micro-Lesson #51
In This Section
Liquids in Microgravity
The simple act of pouring a glass of water from a pitcher needs gravity. The gravity pulls the liquid down in the pitcher and gives it a level surface. Tipping the pitcher brings the spout below that level surface, causing the liquid to flow out of it. Gravity then pulls the liquid downward and into the waiting glass. What do people do when they are in orbit and do not feel the pull of gravity? The answer took many years of study and design.
Next Generation Science Standards (NGSS):
- Discipline: Physical Science
- Crosscutting Concept: Cause and Effect: Mechanism and Explanation
- Science & Engineering Practice: Constructing Explanations (for science) and Designing Solutions (for engineering)
GRADES K–2
NGSS: Matter and Its Interactions: Plan and conduct an investigation to describe and classify different kinds of materials by their observable properties.
NGSS: Motion and Stability: Forces and Interactions: Plan and conduct an investigation to compare the effects of different strengths or different directions of pushes and pulls on the motion of an object.
Fill a pitcher with water and set it down. The water sits in the pitcher, sloshing back and forth slightly from the movement of setting it down, and eventually comes to rest with a level surface. Even if you tip the pitcher slightly, the surface of the water is always level. The reason for this is that the Earth’s gravity is pulling down on the water; if any part of the water’s surface is higher than any other part, the gravity will pull the higher part “downhill” until the surface is completely level. (If you examine this in detail, you will discover that this is not quite true because of capillary action, but that is a small effect.)
In space, however, where people do not feel the pull of gravity, there is nothing to keep the water in the pitcher. The slightest movement of the pitcher will set the water in motion and it will keep moving until it has flowed as far as it can go in whatever direction it started moving.
To keep from making messes in space, people do not store water in open containers. Instead, they keep it in closed bottles with tubes to let it flow from one place to another. This keeps the water from escaping into the room and going places where it should not.
Suggested Activity: Take a washcloth, make it soaking wet, and wring it out. Then watch a video of Space Station astronaut Chris Hadfield doing the same thing in space. Notice the closed water bottle he uses to wet down the washcloth and how the water sticks to the washcloth and his hands rather than dripping down to the floor.
GRADES 3–5
NGSS: Matter and Its Interactions: Make observations and measurements to identify materials based on their properties.
NGSS: Motion and Stability: Forces and Interactions: Support an argument that the gravitational force exerted by Earth on objects is directed down.
Think of all the liquids we use throughout the day for various reasons. We have something to drink with each meal and usually with our snacks. Sometimes the food itself is a liquid, like soup. We often drink water to stay hydrated, especially after exercising. Then there are all the things we clean—washing our hands, taking a bath or shower, doing laundry or washing dishes. Even mopping the floor uses liquid.
Now imagine how all those activities would be affected by microgravity like the environment on the International Space Station. Would a drink stay in the glass or soup stay in the bowl? How would the water behave in a shower or a bathtub on the space station? What about the water in a dishpan or a mop bucket? If you watch the video of astronaut Chris Hadfield wetting a washcloth, you will begin to see the difficulties of carrying out these everyday activities while in space. Can you think of some alternatives that we use here on the planet that would also work on the ISS? Items like no-rinse shampoo that can be toweled off, wet wipes that can be used on hands or surfaces, and other conveniences are all helpful to the astronauts. And they do stay clean, as you can see in this video of Italian astronaut Samantha Cristoforetti.
Those are not the only issues. You can put beverages into a sports bottle or a drink pouch to prevent leaks and spills, but what happens after you drink them? The astronauts do not drink carbonated beverages (sodas like Coca Cola or Pepsi), in space because of the way liquids behave in microgravity. On Earth, we enjoy a cold soft drink and the gas bubbles from the carbonation drift to the top and fizz in the glass or the can. In space, the bubbles stay mixed in the liquid and astronauts would consume much more of this gas than they would on Earth. Also, as the liquid settles into our stomachs and the few gas bubbles rise, we may burp and politely say, “Excuse me.” But without the pull of gravity to make the liquid settle and the bubbles rise, astronauts would have a very uncomfortable and gassy time, because burping in space can be a messy business.
Suggested Activity: Empty a small amount of soda out of an individual serving bottle (12 oz. or 16 oz.), then shake up the bottle to show how the carbonation causes bubbles. Set the bottle down and let the bubbles rise to the top. Then ask the students what it would be like in that bottle if there were no “top” because gravity was not pulling the liquid “down.”
GRADES 6–8
NGSS: Motion and Stability: Forces and Interactions: Construct and present arguments using evidence to support the claim that gravitational interactions are attractive and depend on the masses of interacting objects.
The question of how liquids behave in zero gravity causes concerns beyond water in the spacecraft cabin. Liquid-fueled rockets are fueled by liquids; the rocket itself contains a tank full of fuel and another tank full of oxidizer. While the main stages of the rocket are lifting it through the atmosphere and putting it into orbit, there is an effective “down” direction caused by the thrust of the engines. Once in orbit, however, the spacecraft can be pushed in any direction by the low-thrust maneuvering engines and the thrust cannot be depended on to push the fuel and oxidizer in the tanks toward the pipes leading to the engines.
One way to be sure that the fuel in a tank is pushed toward the outlet pipes is to put a flexible bladder in the tank on the side opposite the pipes. As the liquid—fuel or oxidizer—flows out of the tank, a gas is pumped into the bladder to make it expand. The expanding bladder pushes the liquid out of the way and towards the side of the tank with the pipes. The bladder and tank need to be designed carefully so that the bladder does not push up against the pipe openings while there is still usable liquid in the tank.
Another way to push the fuel or oxidizer in a tank towards the outlet pipes is to use a separate rocket motor with a separate fuel system to create a small acceleration which pushes the liquid in the desired direction. These small rocket motors, called “ ullage motors,” need only accelerate the spacecraft by a thousandth of normal gravitational acceleration to have the desired effect.
Even while the rocket is ascending, the liquid fuel and oxidizer in the tanks can cause concern. The “free-surface effect” causes the liquids to become unstable and to tend to push the rocket off course. To demonstrate the free-surface effect, you can fill a cookie sheet or other very wide, very shallow pan with water. Then try to lift it up and hold it level. Any slight motion to one side or the other causes the water to move towards one side of the pan, increasing its weight on that side and causing you to have to lift up with more force to keep the pan steady. This increased lifting force causes you to raise that side of the pan more, overcompensating and pushing the water towards the other side of the pan. If you are not extremely careful (or sometimes even if you are), you cause the water to slosh from one side of the pan to the other, eventually spilling it over the side.
To counteract the free-surface effect, engineers put baffles in to the tanks. These baffles are plates which stop the liquid from flowing freely all the way from one side of the tank to the other. This reduces the sloshing and keeps the instability down to a manageable level. The use of baffles is not restricted to rockets; automobile gasoline tanks also contain baffles to lessen the amount of sloshing as the car accelerates, brakes, or turns.
GRADES 9–12
NGSS: Motion and Stability: Forces and Interactions: Analyze data to support the claim that Newton’s second law of motion describes the mathematical relationship among the net force on a macroscopic object, its mass, and its acceleration.
When gravitational forces are not important, other forces begin to dominate the flow of water. All of these forces push on the water and cause it to move; some push harder than others. The relative influence of the different types of forces are summarized in a series of dimensionless numbers. For example, the Froude number is the ratio of the gravitational force on a bit of water and its inertia. The formula for the Froude number is
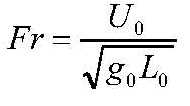
U0 is a typical speed of the flowing water
g0 is the gravitational (or other bulk) acceleration
L0 is a typical length of the waterflow
In a pitcher of water on the surface of the Earth, the typical speed will be quite small, maybe a tenth of a meter per second; the gravitational acceleration will be about ten meters per second squared; and the typical length will be about a tenth of a meter, giving a Froude number of about 0.1. The number is dimensionless; if you express the quantities in English units (U0~ 0.32 ft/sec, g0 = 32.2 ft/sec2, L0 ~ 0.32 ft) you will get the same result of Fr~ 0.1. Small Froude numbers indicate that the gravitational force is important in a flow; large Froude numbers indicate that gravity is not important.
Another dimensionless number is the Eötvös (pronounced “Oot-voos”—the “ö” sounds like the “oo” in “foot”) number, also called the Bond number. This number describes the relative importance of gravity and surface tension in a flow; its formula is
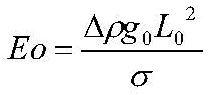
where
Δρ is the density of the water (strictly speaking the difference in density of the water from the surrounding air)
g0 is the gravitational (or other bulk) acceleration
L0 is a typical length of the flowing water
σ is the surface tension of the water
If the Eötvös number is much larger than one, then gravity predominates over surface tension. If it is much less than one, though, surface tension predominates over gravity.
The surface tension of water in air is about 0.07 Kg/s2; the density of water is about 1000 Kg/m3. On the surface of the Earth, where the gravitational acceleration is 9.8 m/s2, a water droplet 0.001 meters (one millimeter) across (just less than a quarter of an inch) will have an Eötvös number of 1000 Kg/m3 × 9.8 m/s2 × ( 0.001 m )2 / 0.07 Kg/s2 = 0.14, meaning that surface tension will pull the droplet into a spherical shape even though gravity is pulling it out flat. In the Space Station video in which astronaut Chris Hadfield wrung out a washcloth about 0.2 meters long in the presence of an exceptionally-small gravitational acceleration (let us use one micro-gravity, or about 0.00001 m/s2, for convenience, although the true number could be smaller by a factor of ten), the Eötvös number is about 0.006. In this case, surface tension is very much more important than gravity in determining how the water flows around Mr. Hadfield’s washcloth.
There are many more dimensionless groups from various fields of science and engineering. Many of them are very specialized; others, like the Mach number, are known by the general public.
Sixty Years Ago in the Space Race:
