Aerospace Micro-Lesson #26
In This Section
Spot the Space Station
The International Space Station is the largest artificial object in space and is the third-brightest object in the sky after the Sun and the Moon. NASA has a web site in which you can enter your geographical location and find out when the Space Station will fly over you and you can see it.
GRADES K–2
I invite you to look up the “Spot the Station” web site, type in your location, and find when the Station will be passing overhead. Look for appearances where the “Max Height” is at least 30 degrees unless you have a very wide-open field from which you can look. The weather needs to be clear. If there is a good appearance of the Space Station in a few days from your location, you can invite the students to go out and look for it from home. There is a certain reality and connectedness that a person gets from actually looking up and seeing the light in the sky that one does not get from looking at a picture.
The “Spot the Station” also tells when and where one can see the supply vehicles that go to and from the Station. These supply vehicles are very small, therefore not nearly as bright as the Station itself.
GRADES 3–5
The Space Station orbits the Earth, moving around once every ninety minutes or so. It shines by reflecting the light of the Sun. For you to be able to see it when you look in its direction, two things need to be true. First, the Sun needs to be shining on the Space Station so that it is lit up. Second, the Sun needs to be below the horizon where you are, so that the rest of the sky over your head is not lit up.
During the day, the Sun is in the sky and its light makes the sky blue. It also makes the sky bright enough that you cannot see the planets or stars; you can barely see the Moon during the day. The sky is also bright enough that you cannot see the Space Station.
The Space Station’s orbit is just over 200 miles above the surface of the Earth. This is about one-fortieth of the Earth’s diameter. If you have a fifteen-inch globe, the Space
Station would be orbiting three-eighths of an inch above its surface. When the Station is on the night-time side of the Earth, it spends most of its time in the Earth’s shadow and so cannot be seen.
The times to see the Space Station, then, are shortly before dawn or shortly after dusk. At those times, the sun has not yet risen or has just set for you, but the Space Station is still in the sunlight. If you have a bright light and a globe, you can illustrate this by holding a “Space Station” off to the side of the globe (relative to the direction to the light).
GRADES 6-8
If a student has a pair of binoculars, he or she could try to find the Space Station using them. The Space Station is about 300 feet long and, at an angle of 30 degrees above the horizon, about 400 miles away. (At higher angles it is closer, coming as close as 200 miles away when it is directly overhead.) You can use some elementary ratios, multiplication, and division to tell whether you can make out any details in its appearance.
The first thing to do is to translate the Space Station’s size into miles. You do this by dividing the length (about 300 feet) by the number of feet in a mile (5,280, which you can round to about 5,000). You get that the Space Station is about three fiftieths of a mile, or 0.06 miles, long.
Now we use ratios. If you have a poster on the other end of your classroom, perhaps 40 feet away, then the apparent length of the Space Station would be the same as the apparent width “w” of something on that poster when you satisfy the ratio:
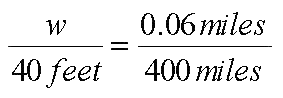
(You can use the fraction instead of the decimal if you like.) The ratio is satisfied when “w” is 0.006 feet (three five-hundredths of a foot). You can convert this to inches by multiplying it by twelve, to get 0.07 inches.
The final multiplication is by the magnification of the binoculars. Binoculars are rated with two numbers with an “x” in between them. The first number is the magnification and the second number is the diameter of the objective lenses, in millimeters. For example, 7 x 40 binoculars magnify the image by a factor of seven. In our case, 0.07 inches multiplied by seven gives an apparent diameter of about 0.5 inches (rounding again).
The bottom line is that if a person can read letters that are a half-inch high on a poster that is 40 feet away, that person can see the Space Station as more than a point of light using binoculars if it is 30 degrees above the horizon. As the Station gets higher in the sky, it comes closer to the observer and it is
easier to make it out.
GRADES 9-12
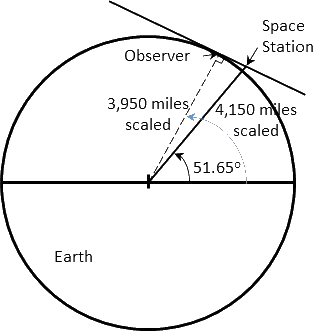
The Space Station’s orbit is inclined 51.65 degrees from the Earth’s equator. Combined with its height of 205 miles above the Earth’s surface, this places a hard upper limit on the farthest north or south a person can be and still see the Space Station. You can calculate this using elementary trigonometry; for students who have not taken trigonometry yet, you can draw a diagram and measure the angle approximately.
To measure the farthest north the Space Station is visible, begin by drawing a circle with a radius of 3.95 inches, or 7.9 inches in diameter. This circle represents the Earth. This scales one inch to one thousand miles. Other scales are possible; you may want to draw only a quarter of the Earth with a circle with a radius of 7.9 inches. On a white board, you can make the circle larger. If you do not make the radius exactly 3.95 inches, it is not important; the answer is not that sensitive to slight errors in the Earth’s radius. Mark the center of the Earth and a horizontal line representing the Equator.
Now draw a line from the center of the Earth to its surface and out beyond the surface, at an angle of 51.65 degrees from the horizontal. (Obviously you will not be able to measure exactly 51.65 degrees; 51 or 52 degrees will do.) This represents the farthest point in the Space Station’s orbit from the equator. Mark a point on this line that is 0.2 inches out from the surface of the Earth; this is the altitude of the Space Station at 205 miles.
The next step is to draw a line that passes through the Space Station and just touches the surface of the Earth at a point farther from the Equator. Mark the point at which this line touches the surface of the Earth; this point is the farthest latitude from the Equator at which an observer can see the Space Station. This is the step that should be done with greatest care; the accuracy of the answer depends the most on the accuracy of this step.
The final step is to draw a line from the observer to the center of the Earth. The angle of this line from the Equator is the farthest latitude north (or south, if you draw it in the opposite direction) from which one can see the Space Station.
If you use trigonometry to find the latitude, the answer is the greatest latitude of the Space Station (51.65º) plus the inverse cosine of 0.9507, which is the ratio of the Earth’s radius (3,956.5 miles) to the Earth’s radius plus the altitude of the Space Station (3,956.5 + 205 miles). The answer is 69.71 degrees.
Sixty Years Ago in the Space Race:
November 6, 1956: The American Navaho missile had its first test flight, which ended in failure 26 seconds after launch because of longitudinal oscillations. The missile was never actually used, although lessons learned during its development were applied to many other rocketry programs.
November 8, 1956 – United States Navy Lt. Comdrs. Malcolm D. Ross and M. Lee Lewis established an altitude record of 76,000 feet during the Strato Lab High I balloon flight.
