Aerospace Micro-Lesson #34
In This Section
Pi Day
The number “π” (written in English letters as “pi” and pronounced “pie,” although the Greek letter in the Greek alphabet is pronounced like the English letter “p”) was originally derived as the ratio of the circumference of a circle to its diameter. The numerical value is just less than three and one seventh; an approximate decimal value if 3.14159. A practice has grown in recent years to celebrate March 14 as “Pi Day,” after the first three digits of the number. (The year 2015 had a special once-in-a-century “Pi Day,” but we are unfortunately too late for that.) “Pi Day” is usually celebrated by eating pie at some point during the day, often at 1:59 to celebrate the next three digits of the number.
Next Generation Science Standards (NGSS):
- Discipline: Engineering, technology, & applications of science.
- Crosscutting Concept: Patterns.
- Science & Engineering Practice: Using mathematics & computational thinking.
Common Core State Standards (CCSS):
- Numbers & Operations in Base Ten: Understanding place value.
GRADES K–2
CCSS: Understanding Place Value: Understand that the three digits of a three-digit number represent amounts of hundreds, tens, and ones.
It would be fun simply to bring in a couple of pies and have a snack.
In the same way that numbers have a ones place, a tens place, a hundreds place, and so on, we can also give them a tenths place, a hundredths place, and so on, going to the right instead of to the left. We put a period (called the “decimal point”) to the right of the ones place to show exactly where the ones place is. As such, the number “3.14” is three ones, one tenth, and four hundredths. The number “π” extends to the right as far as you want to take it, and then some.
GRADES 3–5
CCSS: Understand the Place Value System: Read, write, and compare decimals to thousandths.
As a stunt, some Englishmen used a computer to print out a million digits of “π” on a strip of paper a mile long. Then they unreeled the strip of paper along an airport runway. There is an entertaining You-Tube video of them doing this.
In addition, somebody has translated the first 31 digits of “π” (everything until the first zero) into music. (I believe that he stopped where he did because his musical conversion had no way to translate a zero.) There is a You-Tube video of the result, played as a poly-tempo canon.
There are ways to remember the first several digits of “π” by coming up with phrases made up of words with the appropriate numbers of letters in them. One simple example is the question, “May I have a large container of coffee?” The numbers of letters in each word are 3, 1, 4, 1, 5, 9, 2, and 6. A British physicist a century ago came up with a longer one: “How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics.” There are more.
GRADES 6–8
CCSS: Ratios & Proportional Relationships: Recognize and represent proportional relationships between quantities.
One of the beauties of mathematics is that concepts and items from one branch keep showing up in other branches. As such, “π” shows up in statistics, infinite series, and many other places. One very neat formula involving “π” is:
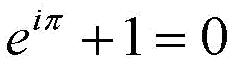
The number “e” has a decimal value that begins “2.718281728” and is used in logarithms.
Exponentiation (shown by the small “i π” up and to the right from the “e” indicates repeated multiplication. The number “i”, when multiplied by itself, is “-1” (called “minus one” or “negative one”), which is the foundation of what is called “complex arithmetic.” Each of these is the basis of a different branch of mathematics, usually taught on a university level. The equation itself reads “e to the i pi plus one equals zero.”
While “π” cannot be represented exactly by a fraction, one can find fractions that approximate “π” quite well. A first approximation, known back to Old Testament times, is simply to use a value of three (see I Kings 7:23 for an example of this). Another very common fraction that students use is 3 1/7 (three and one seventh), expressed as an improper fraction as 22/7, which is good to two decimal places. It has the advantage of including only one-digit numbers. The mathematician Archimedes discovered that 3 10/71 gives an even closer value. The closest approximation using only three-digit numbers is 3 16/113, which is expressed as an improper fraction (and may be easier to remember) as 355/113.
In addition to Pi Day, you can celebrate days that correspond to other mathematical or physical constants. Here are a few suggestions, some more contrived than others:
- February 7 (2/7): e Day. The number “e” has a numerical value of 2.718281828… . A particularly special e Day will come in 2018.
- June 2 (6/02): Avogadro Day. Avogadro’s Number, 6.02214×1023, is the number of items in a mole. A “mole” is like a dozen, a score, or a gross, except that it is larger.
- June 28 (6/28): Tau Day. The number “t” is twice p, although it is much less commonly used. Its numerical value begins “6.283185307”.
- September 8 (9/8): Gravity Day. The acceleration due to gravity on the earth’s surface is about 9.8 m/s2.
If you bring in (circular) pies to celebrate Pi Day, you may want to measure their diameters and circumferences, take the ratio, and see how close to 3.14159… you get. You can make the measurements in inches, centimeters, and millimeters; the ratio will come out the same.
GRADES 9–12
CCSS: The Real Number System: Explain why the sum or product of two rational numbers is rational; that the sum of a rational number and an irrational number is irrational; and that the product of a nonzero rational number and an irrational number is irrational.
The number “π” is an example of a “transcendental number.” Transcendental numbers are the penultimate step in a process that starts with counting numbers and extends them in more and more directions. Counting numbers are “closed” under addition; this means that if we add one counting number to another counting number, the result will always be a counting number. Counting numbers are also closed under multiplication. But counting numbers are not closed under subtraction; if we try to subtract five from three we do not get a counting number.
To correct this, we extend the counting numbers by putting in zero and the negative whole numbers; the result is the set of numbers called the “integers.” Integers are closed under addition, subtraction, and multiplication; if you add, subtract, or multiply two integers, you will always get another integer. They are not closed under division, though; three divided by five does not give an integer result.
So we extend our numbering system to include fractions; the resulting system is called the “rational numbers.” A rational number can be expressed as the ratio of two integers; it can also be expressed as a decimal, either of finite length or with an infinitely repeating pattern. (A finite decimal can be thought of as having a repeating pattern of zeroes after the last nonzero digit.)
This almost does the trick, but the system of rational numbers is still not closed under division; dividing something by zero does not give a rational number as the result. There are two ways to deal with this problem. One is simply to live with it. The other is to include a “point at infinity” as a rational number. Many mathematics teachers maintain strongly that “infinity is not a number” and they are right. Others say that infinity is a perfectly good number; they also are right. One of the beauties of mathematics is that you can make up your own rules and see what you can derive using them. (For teen-agers, you may want to emphasize or omit the “make up your own rules” part.)
The rational numbers are not closed under exponentiation. The ancient Greeks recognized this; the Pythagorean school had a proof that there are no two whole numbers “α” and “b” such that:
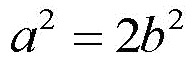
This is equivalent to saying that the square root of two cannot be expressed as the ratio of two integers. More generally, numbers that can be expressed as the solution to a polynomial with rational coefficients are called “algebraic numbers.” They can be expressed as decimals that do not repeat.
After deriving the existence of algebraic numbers, mathematicians realized that there are other numbers that can also be expressed as non-repeating decimals. These are the transcendental numbers; they are best defined as what they are not. They are not integers; they are not rational numbers; they are not algebraic numbers. They are the remaining thicket of numbers that fill out the number line.
At the beginning of this process I mentioned that transcendental numbers are the penultimate step in the process. The last step is to include the square root of negative one, bringing the imaginary and complex numbers into the system. But this is a step beyond the present lesson.
Sixty Years Ago in the Space Race:
March 1, 1957: The first test launch of a Jupiter 1-C rocket ended in failure 72 seconds after liftoff when the rocket overheated and exploded.
March 14, 1957: A Jupiter A missile
was launched successfully.
