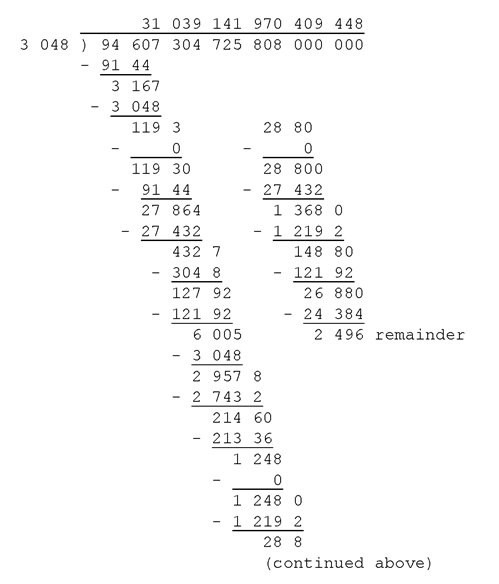Aerospace Micro-Lesson #24

Measuring the Size of the Universe

Astronomers tell us that the universe is about 13.8 billion years old and 93.2 billion light-years in diameter.  How do they know this?  Nobody was there with a clock or calendar at the beginning; nobody has gone out to the edge of the universe with a measuring stick.  This lesson describes some of the methods astronomers have used to arrive at these figures.  A web page at Georgia State University named “Hyperphysics” has excellent background material.  There is also a You-Tube video which is suitable for older students on measuring the size of the universe.

GRADES K–2

Astronomers measure the distances to stars and galaxies by indirect methods.  This means that they measure some other distances and angles and then calculate from their measurements what the larger distances must be.  You can illustrate this sort of indirect reasoning by placing three objects, perhaps something red, something yellow, and something green, on top of a closed shoe box.  Have the kids note the three objects.  Then put something down in front of the box and the objects that hides them and place one of the objects in the box.  Remove the thing that hides the box and the objects and tell the kids that one of the objects is now in the box.  Ask them which one, and ask them how they figured it out.  Obviously (to adults), the one that they can no longer see on top of the shoe box must be the one that is in it.  This is indirect reasoning; they haven’t actually looked inside the shoe box to see the item in it, but they have seen other things and figured it out. 

GRADES 3–5

Distances to stars and galaxies are usually measured in “light-years.”  A light-year is a unit of distance, not of time.  It is the distance that light travels in a vacuum in one year; it is equal to just over 9.46x10¹⁵ meters, or 5.88 trillion miles.  For comparison, light travels from the earth to the moon in 1.28 seconds.  One “light-nanosecond,” which is the distance that light travels in one billionth of a second, is 11.8 inches.  One can illustrate this by holding one’s hands up about a foot apart and saying “about this much.”  A good car will travel one light-second, or 186,282.4 miles, over its lifetime; interested students could ask their parents how close the family car is to reaching this milestone.  There is a “TED-Ed” talk ( also found on You-Tube) in which the speaker spends the first minute or so listing some astronomical distances.

To help students lose their fear of large numbers, you may want to write out the exact value of the number of meters in a light-year:  9,460,730,472,580,800 meters.  You can also point out the places up to the quadrillions.  For students who have had long division and decimals, you can also convert the value to feet by dividing by 0.3048.  You first multiply both numbers by 10,000 to convert “0.3048” to a whole number.  Then the process looks like this:

 

GRADES 6-8:

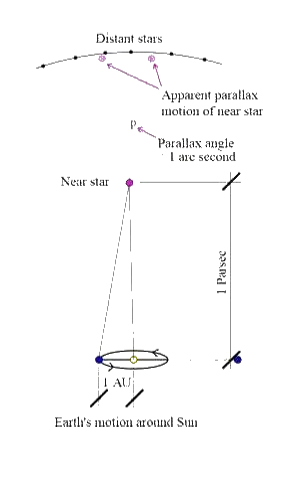
If we know the size of the earth’s orbit, we can measure the distances to the nearest stars.  The astronomers started with the brightest stars, figuring that they would probably be nearer than fainter stars.  The astronomers used the parallax method (described in the Ides of June 2016 lesson) and measured the direction to a relatively nearby star when the earth was on one side of the sun in its orbit and then again six months later, when the earth was on the other side of the sun in its orbit.  The differences in angle are extremely small; the nearest star to the sun is 4.37 light-years away and the change in angle because of parallax is about one and a half arcseconds (or 0.0004 degrees).

Another unit that astronomers use to speak of distances to stars is the “parsec.”  The word “parsec” is short for “parallax second” and is the length of the height of a right triangle whose base is the distance from the earth to the sun and whose angle between the height and the hypotenuse is one arcsecond.  One parsec is equal to about 3.26 light-years.  Scientific American has an excellent You-Tube video which illustrates the use of parallax in measuring distances to stars.

When Copernicus first put forward the theory in 1543 that the earth moves around the sun as the other planets do, one argument against his theory was that the directions to the stars should change as the earth moves and nobody could see any such change.  Copernicus’ theory did not begin to gain an advantage until 1609 when Kepler demonstrated that the planets followed elliptical orbits rather than circular orbits and Newton’s 1666 theory of universal gravitation provided a sound mathematical and physical basis for it.  The theory was not proven until 1838 when Friedrich Bessel successfully measured the parallax of a star.

GRADES 9-12

There is a type of star called the “Cepheid variable” whose brightness changes cyclically over time.  The curve of the star’s brightness as a function of time has a very recognizable sawtooth shape.  Cepheid variables are found with different masses and intrinsic brightnesses, but they all vary in brightness and their curve of brightness as a function of 

time always has the same shape.  What makes them very useful is that the period of the variation, which is the amount of time before the star’s brightness curve repeats itself, varies with the star’s intrinsic brightness.  The star’s apparent brightness, which is the brightness that we can see ourselves, is equal to the intrinsic brightness divided by the square of the distance from us to the star.  Astronomers used Cepheid variables in a nearby galaxy, which are all about the same distance from us, to find the correlation between the period and the intrinsic brightness.  They also measured the distances to the nearest Cepheid variables using the parallax method.  While the parallax method is good for measuring distances only to a few hundred light-years, the Cepheid variables allow astronomers to calculate distances out to twenty million light-years or so.

Other “standard candles” such as globular clusters of stars and supernovae also have relatively uniform intrinsic brightnesses.  By comparing the calculated intrinsic brightness to the observed apparent brightness, astronomers can estimate how far away the “standard candle” is and therefore how far away the galaxy containing it is.  Supernovae allow astronomers to estimate distances out to billions of light-years; the drawback is that a supernova is a very short-lived event and must be observed to be useful.

The final step in calculating the size of the universe is using the red shift of galaxies.  The red shift is a result of the Doppler effect, in which waves emitted by a source that is moving away from you have a longer apparent wavelength.  (You can illustrate the Doppler effect using sound by noticing that the pitch of a car engine or horn changes in pitch from higher to lower as the car passes you.)  Astronomers discovered almost a century ago that galaxies appear to be moving away from each other and that the speed of the apparent motion is proportional to the distance to the galaxy.  Extrapolating the motion back to a zero point (and using some mathematical modeling) gives a result that the universe is about 13.8 billion years old and about 93.2 billion light-years in diameter.

There is a five-and-a-half-minute “TED-Ed” talk ( also found on You-Tube) about measuring astronomical distances.

Sixty Years Ago in the Space Race:

October 1, 1956:  The American Terrapin two-stage solid-fuel sounding rocket had its first flight, reaching 400,000 feet, or over 75 miles.  (Other references give the date of the flight as September 21.).