Aerospace Micro-Lesson #22

The Magnus Effect

The Magnus Effect is a feature of airflow around a spinning body that is also moving relative to the airstream (or that has air flowing over it).  The spinning flow combines with the one-directional flow to produce a net sideways force that, unless balanced out somehow, will push the body to the side. You can see an excellent illustration of the Magnus Effect on You-Tube.

You can also illustrate the Magnus Effect with a ping pong ball and paddle, although it takes a little practice.  What you do is hit the ball with the paddle, but as you are hitting the ball you “slice” the paddle in some direction.  If you “slice” the paddle downwards, you put a back spin on the ball and the Magnus Effect will make it sail farther than it would with a straight hit.  If you “slice” the paddle towards the left, the Magnus Effect will push the ball towards the right; if you “slice” the paddle towards the right, the path of the ball will curve towards the left.

GRADES 3–5

In addition to the ping pong ball and paddle described in the Grades K-2 lesson, the Magnus Effect can be seen in the pitch of a baseball.  When the pitcher throws a curve ball, he makes the ball spin top-to-bottom.  This “top spin” causes the air above the ball to have higher pressure and thus to push the ball downward, causing it to “break” suddenly as it approaches the batter.  NASA’s Glenn Research Center has a quick calculator which allows you to calculate how far the ball will curve.  If your physical education department has a baseball pitching machine, you may be able to use it to illustrate a curve ball.  You can also find videos on You-Tube that show the effect.

If you compare how much a baseball moves away from a regular parabola with how much a ping pong ball moves to the side, you can see that the ping pong ball moves much farther.  This is because it is much lighter than a baseball relative to its size.  Newton’s Second Law says that the acceleration of a body is proportional to the force on it and inversely proportional to its mass; what this means is that for the same force, a lighter body will accelerate more (and thus over time move farther) than a heavier body.

A soccer ball’s “bend” also results from the Magnus force.  ( A second video explains the motion in terms of the air on the low-pressure side being turned toward the other side while the air on the high-pressure side goes straight; this is simply another view of the same effect.)  The effect is more pronounced than the curve ball in baseball but less pronounced than the motion of a ping pong ball because the soccer ball is less dense overall (including the hollow center) than a baseball and denser than a ping pong ball.

The “hook” and “slice” in golf come from the same effect.  This is harder to demonstrate in a classroom or ball field, though.

GRADES 6–8

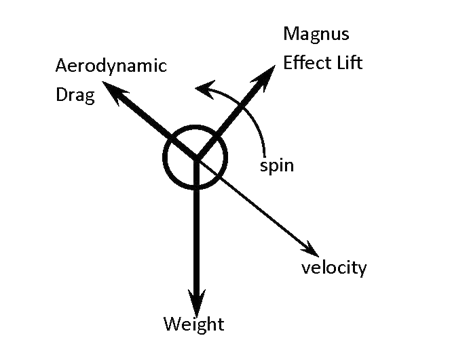
If you watch the basketball video carefully, you will see that path of the basketball curves as it falls downward.  It starts by going straight down, and then as the ball increases in downward speed its path move more away from the vertical direction.  When the ball reaches the stream below the dam, its path is so close to being horizontal that it actually skips across the surface of the water.  As the path of the ball curves, the “sideways” direction turns with it so that by the time the ball reaches the water the combination of the Magnus Effect and the aerodynamic drag is almost pulling it straight upwards.  You can draw a vector force diagram that looks like this:

As the path of the ball curves more away from the vertical, the combination of aerodynamic drag and Magnus Effect lift pull the total aerodynamic force more towards the vertical.

The Magnus Effect is not restricted to the flight of spheres.  A propulsion system for ships called the Flettner rotor was tried out in the 1920s. The Flettner rotor is a vertical cylinder that spins and in a crosswind pulls the ship forward using the Magnus effect. In a decent wind, the energy used to spin the rotors is less than the energy that moves the ship forward and save up to 40 percent of the fuel needed to propel the ship over a simple propeller.

Grade 9-12

Why does the Magnus Effect work? The answer is in our old friend, the Bernoulli Equation. The Bernoulli Equation states that at low speeds and ignoring gravity, the sum of the pressure “P” of a parcel of air (or water—it also holds for liquids) and half the density “ρ” times the square of the speed “V” is a constant:

You can think about this in terms of conservation of energy.  The pressure is a measure of the internal energy of the air; the density and speed term give the kinetic energy of the parcel of air.  The gravity term, if you include it, is the potential energy of the parcel of air.  The equation simply states that the energy of a given parcel of air is constant.

You can also think about the Bernoulli Equation in terms of the motion of the molecules of the air.  The pressure is caused by the molecules of air bouncing off the walls of a container (or off each other, if there is no container).  Each bounce gives a minuscule push on whatever is feeling the pressure.  If all the molecules are moving in the same direction, the air itself that is composed of the molecules is moving in that direction.  The pressure is caused by the random, disordered motion of the molecules. The Bernoulli Equation states that the more that the motion of the molecules is random, causing higher pressure, the less the motion is aligned in one direction, causing a lower speed.

Back on the large scale, consider air flowing past a spinning body.  The friction of the air on the surface of the spinning body tends to drag the air along with the spin.  Where the body’s surface is moving in the direction of the airflow, the spin increases the air’s speed and lowers the air pressure.  Where the body’s surface is moving against the direction of the airflow, the spin decreases the air’s speed and thus increases its pressure.  The imbalance in pressure causes the force which is the Magnus Effect.

Interestingly, if one uses a smooth ball about the same size and weight as a soccer ball, the ball will “bend” in the opposite direction from what one would expect.  The reason has to do with the nature of the boundary layer of the air as it flows over the surface of the ball—laminar versus turbulent—and following the explanation would make a good exercise for more interested students.

Sixty Years Ago in the Space Race:

September 7, 1956: An American test pilot flew his rocket-powered X-2 airplane to a height of 126,200 feet (almost 24 miles).