Aerospace Micro-Lesson #44
In This Section
Rocket Science 101
Everyone knows the saying, “it’s not rocket science,” but what IS rocket science? It turns out that most “rocket scientists” are aerospace engineers and the work that they do to build and launch rockets involves a wide variety of scientific and engineering tasks. Rockets are some of the most complicated and carefully-designed machines ever produced; yet the rocket industry produces and launches them so often that we take them for granted–rockets launch every day lifting astronauts, satellites, and cargo to Earth orbit and beyond. Each of these technological marvels takes hundreds of talented engineers to design, build, and study.
Next Generation Science Standards (NGSS):
- Discipline: Physical Science
- Crosscutting Concept: Energy and Matter
- Science & Engineering Practice: Developing and Using Models
GRADES K–2
NGSS: Motion and Stability: Plan and conduct an investigation to compare the effects of different strengths or different directions of pushes and pulls on the motion of an object.
So what makes a rocket fly? The answer is its engines! If you look at a rocket flying, you will see machinery at the bottom which is creating big flames – these are the engines! Rocket engines are big, complicated things, but the basic idea behind them is pretty simple. To understand this, imagine blowing up a party
balloon (this makes a good classroom demonstration). When you blow it up, you are filling it with air – the air is “squeezed” inside the balloon, so we say that it is at high pressure. If you release the balloon, the air is pushed out at high speed, and the balloon goes flying. Why does this happen? The fast air shooting out of the balloon
literally pushes the balloon forward.
Rockets work in much the same way as the balloon, believe it or not! A rocket’s engines produce lots of hot gas, which shoot out of the rocket. The hot gases moving out of the rocket push it forward and into space, just like the air moving out of the balloon pushes the balloon forward.
The reason the rocket burns its fuel and gets the gases so hot is that the gases need to be under very high pressure for them to push hard against the rocket. (The stretchiness of the balloon in your balloon rocket squeezes the air inside, giving the same effect.) The hotter a gas gets, the higher its pressure. You can show this by leaving an empty water bottle in the refrigerator with its lid off. After the air inside it gets nice and cold, take the bottle out of the refrigerator and put the lid on tightly. As the air warms, it will push outward on the bottle, showing that the bottle is squeezing it. For larger effect, you can put the bottle in a sunny spot.
Suggested activity: Create a class demonstration. There are simple directions for making your own balloon rocket on several sites, like NASA. Or, if you would rather have your students make their own rockets, try these straw rockets instead.
GRADES 3–5
NGSS: Motion and Stability: Plan and conduct an investigation to provide evidence of the effects of balanced and unbalanced forces on the motion of an object.
How do rockets work? The science behind it is simpler than you’d think! A rocket has big engines on the back which shoot out fire and hot gases. These gases moving out the back cause the rocket to move forward because of two scientific principles–pressure and the conservation of momentum.
Pressure describes the way that gases–like air–push on things. If you blow into a pinwheel and make it spin, the pressure of your breath is making it move. The same effect explains how parachutes work–wind pushes against the parachute and slows down whatever is tied to the parachute (like a skydiver). In the case of a rocket, the pressure of the exhaust gases is usually greater than the pressure on the rest of the surface of the rocket and this difference in pressure helps to push the rocket forward.
The other thing which moves rockets forward is momentum. Momentum is a property that things have, like weight or height. Momentum is the product of a thing’s mass and its velocity (speed and direction of motion). It describes how much a moving object wants to keep moving–a mosquito buzzing around won’t have a lot of momentum because it’s small and slow, but a truck on the highway will have lots of momentum. Science dictates that the total amount of momentum in a group of objects must always stay the same unless something pushes on them from the outside–kind of like weight (you can’t suddenly make yourself weigh less, can you?). So when a rocket’s exhaust gases leave the rocket in a huge plume of fire out in space (carrying some momentum with them), the rocket has to gain momentum in the other direction. One good experiment which you can do to show how the conservation of momentum works is to sit on a wheeled office chair and throw a ball into the distance. Make sure that the chair is free to roll and that your feet are off the ground, and you should start moving slowly in the direction opposite to the ball – you have given the ball momentum away from you, so you must move backward to compensate. You can probably imagine that if you had a bucket full of balls, you could move yourself around by throwing them behind you; funnily enough, this is exactly how a rocket works–by burning fuel (i.e. “balls”) and shooting it out the back at high speed.
Although both pressure and momentum contribute to a rocket’s thrust, the momentum is a much stronger influence. A simple demonstration which illustrates both pressure forces and the conservation of momentum is the humble party balloon. If you blow it up and release it, you can see the fundamentals of rocket thrust in action–the momentum of the air being forced out of the balloon, and the (comparatively small) effect of the pressure pushing on the balloon.
Suggested Activity: to show how rockets lift a payload, try this Heavy Lifting activity from NASA.
GRADES 6–8
NGSS: Motion and Stability: Plan an investigation to provide evidence that the change in an object’s motion depends on the sum of the forces on the object and the mass of the object.
You can read about the fundamental physics of rocket thrust in the above sections, but the gist of it all is this: rockets work by expelling hot exhaust gases; the gases exert a pressure on the rocket to push it forward, and pushing the weight of the gases backwards propels the rocket via the conservation of momentum.
This latter idea – the conservation of momentum – is actually one of the most important concepts in physics; it is a restatement of something with which you may already be familiar – Isaac Newton’s second law of motion. The second law is usually stated as “force equals mass times acceleration” – meaning, that if we apply a force to an object (i.e. we push on it), it will increase its speed at a rate proportional to its mass (how much matter it contains). To put that more simply – as long as we apply a force to an object, it will continue to move faster and faster, and light objects are easier to push than heavier objects.
The other way to think about the second law is in terms of momentum – in addition to the familiar “force equals mass times acceleration,” we can say that the force exerted on an object is equal to its change in momentum. Mathematically, we get momentum by multiplying an object’s velocity by its mass. Obviously, a big object moving really quickly (like a freight train) will have a lot of momentum, but even a small object can have a lot of momentum if it moves quickly. The exhaust gases of a rocket weigh almost nothing (about as much as air) but since they are moving so quickly (thousands of miles per hour), they have a lot of momentum. This is where a rocket gets thrust to push it through the air and into space! By expelling momentum downwards with its hot exhaust, the rocket is pushed upwards.
GRADES 9–12
NGSS: Motion and Stability: Analyze data to support the claim that Newton’s second law of motion describes the mathematical relationship among the net force on a macroscopic object, its mass, and its acceleration.
If you have read through the above sections, you probably have a decent idea of the fundamentals of rocket propulsion. With this understanding, we can derive one of the most fundamental relations in rocketry – the thrust equation. We begin by drawing a “free body diagram” (a picture showing the forces and where they are applied) of a rocket in flight.
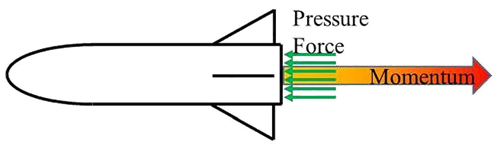
We want to find an expression for the thrust which is driving the rocket forwards; we know that along the primary axis of the rocket, we have the force of the rocket’s exhaust gases pushing on the rocket; we also know that as the exhaust is forced out of the engines, momentum is leaving the rocket (this is not itself a force, but is shown on the free body diagram for completeness).
Newton’s Second Law tells us that the net force on an object is equal to the product of its mass and its acceleration. With a change in the object’s mass, we consider the rate at which momentum is leaving the object to be a fictitious “force.” (Formally speaking, we could invoke Euler’s First Law, which generalizes Newton’s Second Law to include variation in mass and which states that the net force on an object is equal to the rate of change in its momentum.) We express Newton’s Second Law as:
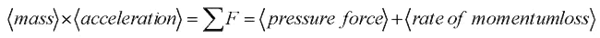
We can write each of these terms as follows:
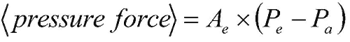
where Ae is the exit area of the rocket’s engines (the area over which the pressure force is acting), Pe is the exit pressure of the exhaust gases, and Pais the ambient atmospheric pressure (zero when the rocket is in space). The rocket’s exhaust exerts a pressure on the rocket, but the ambient atmosphere does as well, which is why we need to take the difference of the two pressures. The momentum term is written as:
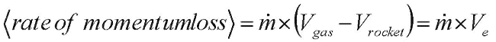
where ṁ is the mass flow rate (amount of mass per unit time) exiting the engines, Vgas is the velocity of the exhaust gas after it leaves the rocket, Vrocket is the velocity of the rocket, and Ve is the exhaust velocity of the rocket, which is part of the rocket’s specification.
Combining these relations yields:
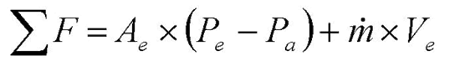
This is the thrust equation – a fundamental principle in studying rockets which provides the thrust (net propulsive force) acting on a rocket. Let’s look at each term.
The momentum term describes the rate at which momentum is being ejected from the rocket through the exhaust.
The pressure term describes how pressure forces act on the base of the rocket – note that it can be either positive or negative. As the rocket moves through the atmosphere, the ambient pressure changes; on the ground, the pressure term is negative and decreases engine performance; at high altitudes and in space, there is no ambient pressure so the higher pressure of the rocket exhaust provides a boost.
You can see how even starting with a basic principle (like Newton’s second law of motion) and a free-body diagram, we can derive a useful equation that helps us study real physical situations – like a rocket! The thrust equation provides a useful estimate of how much force a rocket will be able to generate. Engineers use the thrust equation when designing rockets to understand how the rocket will accelerate and how much weight it will be able to carry.
Sixty Years Ago in the Space Race:
August 8, 1957: The Americans launched its third and final sub-orbital Jupiter-C rocket to an altitude of 285 miles to test a re-entry vehicle.