Aerospace Micro-Lesson #48

Regular Geometric Figures

Regular geometrical figures would seem to be fairly simple, perhaps even boring.  As with most things mathematical, though, there are hidden depths that one can find if one looks closely.  While not directly related to aerospace matters, considering regular geometrical figures encourages abstract thought and the search for patterns in data.

Common Core State Standards (CCSS):

• Math Domain: Geometry

GRADES K–2

CCSS Geometry: Analyze, compare, create, and compose shapes.: Analyze and compare two- and three-dimensional shapes, in different sizes and orientations, using informal language to describe their similarities, differences, parts (e.g., number of sides and vertices/"corners") and other attributes (e.g., having sides of equal length).

Draw an equilateral triangle.  Then draw a square next to it.  What do they have in common?  The sides of both are all the same length and the corners of both are all the same shape.  Figures that have these properties are called “regular polygons.”

You can draw regular polygons with more sides as well.  A regular polygon with five sides is called a pentagon, with six sides is called a hexagon, and with seven sides is called a heptagon.  You can draw a regular polygon with two sides but it doesn’t look much like a polygon; it is just a straight line going from one “corner” to the other and back again.

Another interesting fact about these shapes is that they can all be divided in half. Since the sides are all of the same length, it is easy to find the center and draw a line that cuts the shape into two equal pieces. We call that the line of symmetry and those kinds of shapes can be described as symmetrical.

Suggested Activity: Take a shape walk around your school. What examples of regular polygons can you find? You may wish to have students bring a clipboard and paper to draw their finds, or you may prefer to keep a list yourself. When you return to the classroom, look at your results and discuss which shape was seen most/least often, what was the largest shape you found, and other details that caught your students’ attention. They may even have examples that they recall from other locations outside school.

GRADES 3–5

CCSS Geometry: Classify two-dimensional figures into categories based on their properties: Understand that attributes belonging to a category of two-dimensional figures also belong to all subcategories of that category. For example, all rectangles have four right angles and squares are rectangles, so all squares have four right angles.

The name "polygon” comes from the Greek words “polys” (“πολυσ” in the Greek alphabet), meaning “many,” and “gonia” (“γωνια” in the Greek alphabet), meaning “angle.”  (Be careful with the “gonia” transliteration; the Greek alphabet has two letters for the English letter “o.”)  Why do our words in geometry have Greek roots?  It is because the most influential mathematician was an ancient Greek named Euclid.

The Greek roots are also used in the names of the individual figures.  Here is a list of the Greek words for the different numbers and the names of the polygons:

 

The words “triangle” and “square” are used commonly enough that they come from different sources.  The word “triangle” comes from the Latin “tri” meaning “three” and “angulus” for “corner.”  The word “square” comes from the Latin “exquadrare” meaning “to set in order,” although that word has further roots in the Proto-Indo-European word “qwertwer” meaning “four.”

It is well known that the measures of the angles inside an equilateral triangle add up to 180 degrees and the measures of the angles inside a square add up to 360 degrees.  These actually hold true for any triangle and quadrilateral.  They are the first two steps in a pattern:  the measures of the angles inside a polygon of any number of sides add up to 180 degrees times the number of sides less two.  Thus the measures of the angles inside a pentagon add up to 540 degrees, those inside a hexagon add up to 720 degrees, and those inside an octagon add up to 1080 degrees, and so on.

Suggested Activity: Paper Models of Polyhedra  are available to print out and have your class assemble. Both Platonic and Archimedean solids are provided.

GRADES 6–8

CCSS Geometry: Solve real-world and mathematical problems involving area, surface area, and volume: Represent three-dimensional figures using nets made up of rectangles and triangles, and use the nets to find the surface area of these figures. Apply these techniques in the context of solving real-world and mathematical problems.

The idea of regular polygons extends into three dimensions.  The three-dimensional extension of a polygon is the polyhedron.  (The word “polyhedron” is derived from the Greek words “polys” or “πολυσ,” meaning “many,” and “edra” or “εδρα,” meaning “seat.”  The plural of “polyhedron” is “polyhedra” in a nod to its Greek roots.)  To be a regular polyhedron, a solid must have flat faces; the faces must all be the same regular polygon; and the same number of faces must meet at each vertex.

There are five convex regular polyhedra, also called the Platonic solids.  They are the tetrahedron (with four faces), the hexahedron or cube (with six faces), the octahedron (with eight faces), the dodecahedron (with twelve faces), and the icosahedron (with twenty faces).  (There are four additional regular polyhedra but their faces intersect each other and they are not as easy to visualize.) Students who are active in role-playing games are probably familiar with these shapes from the dice they use to generate character stats and for other actions during the game.

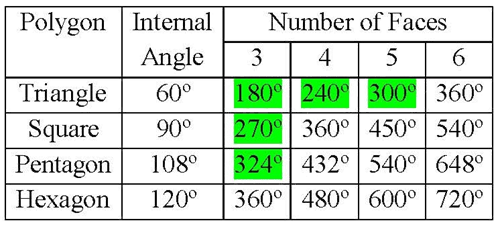
The first remarkable fact about the regular polyhedra is that there are so few of them.  There are infinitely many regular polygons but the number of regular polyhedra is strictly limited to five.  A little thought reveals the reason.  At every vertex, where the different faces come together, the sum of the angles in each face must be less than 180 degrees.  If the angles add up to 180 degrees, you have a tessellation on a flat plane instead of a polyhedron.  We can make a table of polygons, their inside angles at each corner, and the total angle when they come together at a vertex.  Our table starts with three polygons because that is the smallest number of faces that can come together at the vertex of a polyhedron.

The only entries in this table with total internal angles less than 360 degrees are three triangles (which make a tetrahedron), four triangles (octahedron), five triangles (icosahedron), three squares (cube), and three pentagons (dodecahedron).  There are three entries in the table with total internal angles exactly equal to 360 degrees, being six triangles, four squares, and three hexagons; these shapes will tessellate a plane.

If one relaxes the requirements for a “regular polyhedron” somewhat and specifies only that the faces all be the same size and shape, other figures are possible.  Chief among these is the rhombic dodecahedron, which is composed entirely of rhombuses.  A rhombus is not a square, although all of its sides are the same length, and the vertices of a rhombic dodecahedron alternate between having three and four faces come together.  The rhombic dodecahedron is the special case of a “stellated cube,” which is a cube whose faces have all been replaced by pyramids.  If one specifies that the triangular sides of the pyramids are equilateral triangles, the shape becomes a rhombic dodecahedron; otherwise one gets a figure with 24 faces, each of which is an isosceles triangle.  One can also make semi-regular polyhedra by adding pyramids to the faces of other Platonic solids.  Other semi-regular polyhedra are the Archimedean solids and the Quasiregular Polyhedra.

GRADES 9–12

CCSS Geometry: Visualize relationships between two-dimensional and three-dimensional objects: Identify the shapes of two-dimensional cross-sections of three-dimensional objects, and identify three-dimensional objects generated by rotations of two-dimensional objects.

The extension of two-dimensional polygons into three-dimensional polyhedra continues into higher geometrical dimensions.  Just because four-, five-, or six-dimensional spaces do not exist in real life is no barrier for mathematicians thinking about them.  As a bare minimum, one can use the notion of coordinates to describe these higher-dimensional spaces.  The position of a point on a line can be specified by one coordinate; on a plane its position can be specified by two coordinates; in three-dimensional space it can be specified by three coordinates.  To specify the position of a point in a four-, five-, or six-dimensional space one simply uses four, five, or six coordinates.  Indeed, mathematicians have been known to think about spaces with an infinite number of dimensions.

The generalized equivalent of a polygon or polyhedron is called a “polytope.”  Just as a polyhedron has faces that are polygons, an N-dimensional polytope has “facets” that are polytopes of N–1 dimensions.

The simplest polytope to imagine (and specify) in higher dimensions is the hypercube.  A four-dimensional hypercube has its own name:  “ tesseract.”  To generate a tesseract one starts with a one-dimensional line segment and moves it in the direction of the second dimension, making a square.  One then moves the two-dimensional square in the direction of the third dimension, making a cube.  Then one moves the three-dimensional cube in the direction of the fourth dimension, making a tesseract.  Obviously one cannot do this in reality, but mathematically the process is simple.

A tesseract is usually represented as a cube within a cube; this is the three-dimensional analogy of what one gets by shining a flashlight on a wireframe cube and projecting the image on a screen.  The square nearest the light casts a larger shadow than the square opposite it, making the shadow of the cube look like a square inside a larger square with their corners connected to each other.  In the same way, the projection of the four-dimensional tesseract into three-dimensional space is shown as a cube inside a larger cube with their corners connected to each other.

An interesting exercise may be to figure out how many vertices, edges, faces, three-dimensional facets, and so on a hypercube of N dimensions has.  Following the process of building a tesseract from a point, a line, a square, and a cube is instructive.  Every vertex is moved from its starting position to its ending position so the number of vertices doubles.

Every edge is moved from its starting position to its ending position; in addition, every vertex traces out a new edge as it moves; thus the number of edges in the N+1-dimensional polytope is equal to twice the number of edges in the N-dimensional polytope plus the number of vertices in the latter.

A second class of polytope is the higher-dimensional equivalent of the triangle or tetrahedron, called the “simplex.”  This also is relatively simple to generate and visualize.  To generate an N+1-dimensional simplex from an N-dimensional simplex, one places a point in N+1-dimensional space (adds another coordinate to the list of coordinates) equally distant from all the existing points and then draws an edge from each existing point to the new point.

The limitation on the number of regular polyhedra in three dimensions extends into the higher dimensions as well.  In four dimensions there are six convex regular “polychora” (four-dimensional polytopes) and ten more that are not convex.  In five or more dimensions, there are only three regular polytopes per dimension:  the simplex, the hypercube, and the cross polytope.

Sixty Years Ago in the Space Race:

October 23:  The American Vanguard TV-2 was launched to an altitude of 109 miles and landed 331 miles downrange.