Aerospace Micro-Lesson #54
In This Section
Make Your Own Telescope
One usually thinks of telescopes as professionally-made precision instruments—and a good telescope certainly is. Larger telescopes even have their own buildings, called observatories. It is possible, however, to create one’s own telescope very easily with a pair of magnifying glasses. You do not even need a tube.
Next Generation Science Standards (NGSS):
- Discipline: Physical Science
- Crosscutting Concept: Scale, Proportion, and Quantity
- Science & Engineering Practice: Constructing explanations and designing solutions
Common Core State Standards (CCSS):
- Geometry: Modeling with geometry
GRADES K–2
NGSS: Waves and Their Applications in Technologies for Information Transfer: Plan and conduct investigations to determine the effect of placing objects made with different materials in the path of a beam of light.
The basic part of a telescope is a magnifying glass. You can show the kids a magnifying glass and point out that it makes objects look larger if you look at them through it. You can point out that they need to hold the magnifying glass a certain distance from the object for them to see it clearly. When an object looks clear in a magnifying glass, we say that it is “in focus.” When it looks blurry, we say that it is “out of focus.”
There are several stories about the invention of the telescope. One of them recounts that there was a Dutch eyeglass maker about 400 years ago named Hans Lippershey (pronounced in Dutch as “Lippers-hey” rather than “Lipper-shay”). The story goes that his son wanted him to come out to play. He was busy, though, and so he gave his son a bag of old eyeglass lenses to play with. The son took them outside. He picked two of them up and held one in front of his eye and the other at some distance. Moving the far one back and forth, he suddenly saw the weather vane on top of the next building, larger than it usually looked and upside down. He ran back inside and told his father, who also looked through the lenses and realized that this was an important discovery. Whether or not the story is true—and there is considerable doubt about it— it is quite well established that Hans Lippershey was the first person to apply for a patent for a telescope. Rice University has an excellent article on the invention and development of the telescope.
Suggested Activity: You can also use a magnifying glass to cast an image of a light source on a piece of blank paper. The light source can be the classroom window, a ceiling light, a lamp, or just about anything else. (It can also be the Sun, although this is not recommended as it will probably singe the paper and, if the lens is large enough, cause the paper to burst into flame.) You need to hold the magnifying glass a specific distance from the paper in order for the image to be in focus; this distance is called the “focal length” of the magnifying glass. The image will also be upside down if it is of a window, or rotated 180 degrees if it is of a ceiling light. (You can demonstrate this by putting your hand in the way of the light on one side and seeing that the image of the hand appears on the other side of the image.)
GRADES 3–5
NGSS: Waves and Their Applications in Technologies for Information Transfer: Develop a model to describe that light reflecting from objects and entering the eye allows objects to be seen.
To make a basic refracting telescope, you take two magnifying glasses. While it is better that the magnifying glasses have different focal lengths, it is not necessary. (It may be difficult to find magnifiers with different focal lengths, as most of them tend to stick to just one standard length. Some magnifiers have a second “lens-within-a-lens” which will fill the bill.) Hold one magnifier up in front of your eye; to get a telescope that actually magnifies it needs to be the magnifier with the shorter focal length. Hold up the other magnifier at some distance in front of your eye and look through the two magnifiers at some distant object. (DO NOT look at the Sun like this; it will blind you.) Move the second magnifier toward and away from your eye until the distant object appears in focus (and it will be upside down). Voilà! You have just made a telescope.
There are two main types of telescope: refracting telescopes and reflecting telescopes. What sets them apart is how the light is “bent” from parallel rays to rays that come together at a focal point. In a refracting telescope, the light is “bent” by a lens such as the second magnifying glass in the home-made telescope. In a reflecting telescope, the light is “bent” by a concave mirror. There are several different types of reflecting telescope ( Newtonian, Cassegrainian, and others), but they all have the first concave mirror. There are also hybrid telescopes such as the Schmidt-Cassegrain and the Maksutov telescopes that use both lenses and mirrors.
Suggested Activity: Procure some magnifying glasses. Measure the focal length by focusing the image of a distant light or from a window on a piece of paper and measuring the distance between the lens and the paper. Uses two magnifying glasses of different focal lengths to make a rudimentary telescope.
You can also make a rudimentary reflecting telescope using a magnifying glass and a makeup mirror. The focal length of a makeup mirror tends to be a bit longer than arm’s length (mine was about three feet), though, so you will need to set it up somewhere appropriate. Make sure the mirror is showing something in the distance behind you (NOT the sun!) and hold up a magnifying glass to your eye. Move the magnifying glass back and forth until you see a clear image.
Makeup mirrors are not usually ground to a perfectly paraboloidal shape, though, and the quality of the image will probably be dreadful. Magnifying glasses are a little better, though not by much, and so the image will still leave quite a bit to be desired. Even so, a telescope that you make in this way will probably be better than the one that Galileo used to make his first observations. It will certainly have a larger aperture.
GRADES 6–8
NGSS: Waves and Their Applications in Technologies for Information Transfer: Develop and use a model to describe that waves are reflected, absorbed, or transmitted through various materials.
A telescope works when light rays from a distant object come in through the objective lens or hit the primary mirror. The light rays are almost parallel because the object is so far away. The lens or mirror bends the light rays—either by refraction (as they pass through the lens) or reflection (as they bounce off the mirror)—so that they converge to a single point. This point is the “focal point” of the lens or mirror. Passing through the focal point (and perhaps bouncing off an auxiliary mirror) the light rays diverge and then pass through the eyepiece, which is the second lens in the telescope. The eyepiece bends the rays again so that they are parallel again. Here is a web page showing how light moves through different types of telescope.
Three quantities are important in an astronomical telescope’s working. The first is its magnification, which measures how much larger it makes distant objects look. (This is also important—and is by far the most important for other types of telescope such as field glasses.) The magnification is controlled by the ratio of the focal lengths of the objective lens or mirror and of the eyepiece.
The second important point in an astronomical telescope is its ability to gather light. If an object’s apparent size is magnified by a factor of eight, all the light from the object has been spread out over an area 64 times that of the object itself, and the object appears 64 times dimmer than it otherwise would. This is a limiting factor for many astronomical objects; the Great Nebula in Orion, for example, covers twice the diameter of the Moon in the sky but is largely invisible because it is so dim. The Crab Nebula, which is completely invisible to the unaided eye, covers about one quarter the diameter of the Moon in the sky.) A telescope can make up for this by gathering all the light that comes in through the objective lens and concentrating it in the observer’s eye. The telescope’s ability to do this depends on the diameter of its objective lens or primary mirror, called “aperture”; this is why astronomical telescopes are usually described first by this diameter.
The third important point is the telescope’s resolving power. The resolving power is the telescope’s ability to distinguish between two points of light that are close to each other. As one increases the magnification in a telescope by using eyepieces of shorter and shorter focal length, points of light become blurry for a variety of reasons. Increasing the magnification further will simply make them larger blurs. If all other sources of blurriness (imperfections in the optics, atmospheric variation, and the like) are removed, the remaining limit on the telescope’s resolving power comes from its diameter and the wavelength of light. When it is the limiting factor, a telescope’s resolving power increases as its diameter increases.
If one is buying or building an astronomical telescope, one must also consider other factors that are not immediately obvious. For example, to be useful an astronomical telescope needs a solid mount so that one can control the direction in which it points. Sky and Telescope has an excellent guide on what to look for in buying a telescope.
GRADES 9–12
NGSS: Waves and Their Applications in Technologies for Information Transfer: Use mathematical representations to support a claim regarding relationships among the frequency, wavelength, and speed of waves traveling in various media.
CCSS: Modeling with Geometry: Apply geometric methods to solve design problems (e.g., designing an object or structure to satisfy physical constraints or minimize cost; working with typographic grid systems based on ratios).
Deriving the magnification of a telescope is a fairly simple exercise and can show the students a use for their analytic geometry. We begin by drawing an (x, y) coordinate system with the larger lens on the left at an x-coordinate of “–FL” (the focal length of the left-hand lens) and the smaller lens at an x-coordinate of “FR” (the focal length of the right-hand lens).

Consider a light ray coming in from the left. It will follow a straight-line path with a slope “m1” which we can describe with the equation:

We specify that the ray hits the left-hand lens at a y-coordinate of “yL”. (For the purposes of this calculation, the lenses are infinitely thin. This is an approximation.) This allows us to specify the constant “b”:
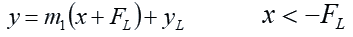
The left-hand lens focuses light coming in from the left with zero slope at its focal point. If the light coming in from the left is horizontal, with a zero slope, then the point at which it focuses is the origin, with a y-coordinate of zero and a distance “FL” from the lens. Thus the change in slope “DmL” of a ray of light hitting the left-hand lens at a y-coordinate of “yL” is:
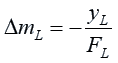
Our ray of light that follows the line of “y = mL ( x + FL ) + yL” will have a new slope “m2” when it has passed the left-hand lens:
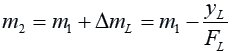
The ray passes through the point ( – FL, yL ) and so follows the line with the equation:
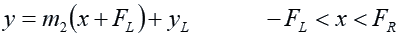
The ray hits the right-hand lens at the point x = FR. Its y-coordinate at that point is:
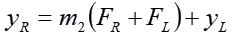
Similar to the left-hand lens, the right-hand lens bends a horizontal ray of light that hits it at “yR” so that it passes through the focal point. The change in slope is therefore:

To the right of the right-hand lens, the ray of light (which hit the lens at ( FR, yR) ) will follow a line with the equation:
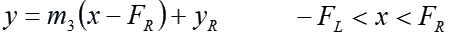
The slope of the line, m3, is given by the formula:
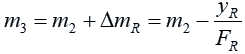
Now let us express m3 in terms of the known quantities. We substitute for yR:
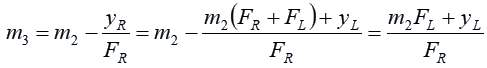
Now we substitute for m2:
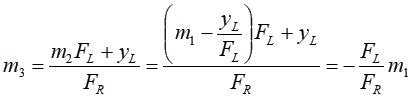
For small angles, the slope of a line is proportional to its angle from the horizontal. What this means is that whatever angle the ray of light is coming into the objective lens at is multiplied by the ratio of the lenses’ focal lengths to give the angle at which the ray of light comes out
of the eyepiece. The apparent size of an object is given by the angle between a ray of light coming from one side of it and a ray of light coming from its other side. A telescope increases this angle, and thus magnifies the object, by a factor equal to the ratio of the focal lengths of the two lenses. The minus sign in the ratio means that the
object appears to be upside down.
In this derivation, it is critical that the distance between the lenses be equal to the sum of their focal lengths. If the distance between the lenses is some other value, then the “yL” does not cancel out of the equation and the final angle depends on where on the objective lens the ray of light falls. In this case, the object is seen in the telescope as being out-of-focus and blurry.
Sixty Years Ago in the Space Race:
January 31: The American Explorer 1 became the first American spacecraft successfully launched into orbit.
