Aerospace Micro-Lesson #69
In This Section
Lifting Bodies
Can you imagine an airplane with no wings? It might sound nonsensical, but the idea – known as a lifting body – is a serious engineering concept which has been around since at least the 1960s. Lifting bodies work because at very high velocities, they produce enough lift to keep themselves airborne. They are pretty inefficient as airplanes, but they make an appealing concept for spacecraft which have to re-enter Earth’s atmosphere as they are lightweight and rugged yet versatile and maneuverable. NASA has flown five different lifting body designs, some of which are shown in the image below, and a company called the Sierra Nevada Corporation is currently building one to ferry supplies to the International Space Station.
Next Generation Science Standards (NGSS):
- Disciplinary Core Ideas: Engineering, Technology and Applications of Science
- Crosscutting Concept: Structure and Function
- Science & Engineering Practice: Constructing Explanations and Designing Solutions.
GRADES K–2
NGSS: Engineering Design: Develop a simple sketch, drawing, or physical model to illustrate how the shape of an object helps it function as needed to solve a given problem.
When we think of airplanes, we usually think of flying machines with big long wings that soar gracefully through the sky. As you may know, wings are what allow most airplanes to fly; as they move through the air, they produce lift—an upwards force which holds the plane up. You’ve probably seen planes with all sorts of wings—long, skinny wings, short, triangular wings, fat, rectangular wings, and more. The variety of possible wing shapes is endless–different shapes produce different characteristics which affect how a plane will fly. However, you may be surprised to learn that airplanes can even be built with no wings at all!
How can a plane fly with no wings? Well, although wings are designed specifically to produce lift, just about any shape can produce at least some lift. Objects generate lift as air flows around them. Under the right conditions, almost anything can produce lift. One good example is a baseball. Baseball pitchers can throw pitches which curve–the ball seems to change direction in midair. The reason for this is because the ball is producing lift–so as it moves through the air, it is pulled in one direction or another. Another example is the effect of putting back spin on a ping pong ball; the lift that is created by the rotation makes the ball fly much farther. Here is an example of the same effect caused by a spinning basketball falling a great distance.
In a normal airplane, even though the wings produce most of the lift, the body of the plane produces some lift, too. A lot of high-speed aircraft rely on this idea to fly with very short wings, as short wings are easier to build and harder to break; at high speeds, an aircraft produces more lift so the wings don’t have to be as large. Back in the 1960s, NASA experimented with an even more radical idea: airplanes with no wings. These airplanes—called lifting bodies—were designed to fly at very high speeds, like spacecraft returning to Earth. In fact, they could only fly at high speeds; at low speeds, they didn’t produce enough lift to stay airborne. However, by moving quickly, these radical-looking vehicles could be flown almost like normal airplanes.
GRADES 3–5
NGSS: Motion and Stability: Forces and Interactions: Make observations and/or measurements of an object’s motion to provide evidence that a pattern can be used to predict future motion.
You probably know that an airplane’s wings are what allow it to fly—air flowing over the wings produces lift, a force which pushes the plane up into the sky. But did you know that it’s possible to build and fly airplanes that have no wings at all? It sounds strange, but it’s true. To understand how these airplanes fly, we need to understand a little bit more about lift itself and the ways in which air exerts forces on flying objects.
Airplane wings have a special shape which creates a difference in pressure between the top and the bottom surface. What does this mean? It means that the air flowing past the wing is pushing harder on the bottom and on the top, forcing the wing upwards. An airplane’s wing is specially designed to create a large force, but any object will feel a lift force if the air flowing around it isn’t symmetric. For example, look at the two photographs at the top of the next page. They are images recorded in a tool called a water tunnel, and they show how water (or air) moves around different objects. The object in the left picture is a flat plate and the object in the right picture is a cylinder.
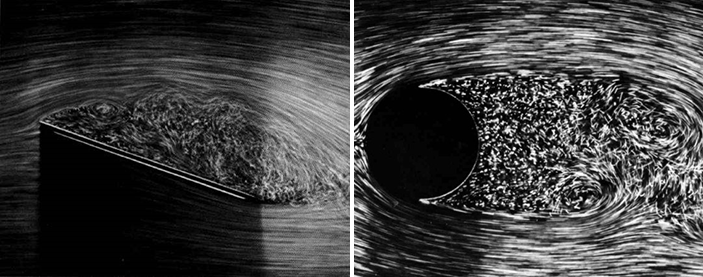
Although the shadows make it a bit difficult to see, the flow around the cylinder is almost perfectly symmetric: the water splits at the front (on the left edge), flows around the cylinder, and rejoins at the rear. In contrast, the flow around the flat plate is very asymmetric: it is fairly smooth on the bottom, but over the top of the plate the fluid is deflected upwards significantly. This should produce a lift force, as the asymmetric flow will produce different pressures on the top and the bottom.
We can use the same principle to create airplanes with no wings called lifting bodies. As long as the aircraft is designed to create an asymmetric airflow, it should produce some lift. Since lift increases at higher speeds, even a small amount of “lifting ability” will allow a lifting body to fly if it travels quickly enough. The lifting bodies which NASA flew in the 1960s needed to travel at about 200 mph to produce enough lift to fly!
GRADES 6–8
NGSS: Motion and Stability: Forces and Interactions: Plan an investigation to provide evidence that the change in an object’s motion depends on the sum of the forces on the object and the mass of the object.
How can an airplane fly without wings? The short answer is “speed”. Although the mechanics of flight can be quite tricky, we can describe lift—the aerodynamic force which allows things to fly—using a simple equation:
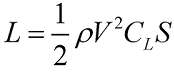
In this equation, L is lift force, ρ is the air density, S is the area of the lifting surface, CL is the lift
coefficient—a value which describes how effectively the surface creates lift—and V is velocity, or speed. We can use a typical plane, such as a business jet, as an example to see how this works (note: values below are approximate, based on the Learjet 75). For level flight, the lift produced by the wings equals the weight of the airplane.
Lift: 96,000 N
Air density: 0.5 kg/m3 (at about 20,000 ft altitude)
Maximum lift coefficient: 1.5
Wing area: 30 m2
Minimum velocity (from equation): 92 m/s
In this example, the plane must fly no slower than 92 m/s (about 200 mph) for its wings to generate enough lift to keep it in the air. Airplane wings are relatively large and quite good at producing lift, but almost any object can produce some amount of lift as the air moves over it (see the above section for a more thorough explanation of this)—just not quite as efficiently as a wing. Some vehicles, creatively named lifting bodies, are designed to fly with no wings at all. Since lifting bodies produce lift much less efficiently than winged aircraft (meaning that they produce more drag for a given amount of lift) and have much smaller lifting areas, they must fly much, much more quickly to stay airborne. For example, consider the HL-20, a concept developed by NASA in the 1990s. We can apply the lift equation just as we did above:

Lift: 103,500 N
Air density: 0.001 kg/m3 (at about 150,000 ft altitude)
Maximum lift coefficient: 0.4
Body plan area: 60 m2
Minimum velocity (from equation): 3,000 m/s
To produce enough lift to fly at its higher altitude, the lifting body must fly at 3,000 m/s – that’s well over 6 thousand miles per hour, or roughly ten times the speed of sound! This might sound crazy, but the high speed requirements of these vehicles make them an ideal concept for spacecraft. Spacecraft must re-enter the Earth’s atmosphere at incredibly high speeds, so lifting body designs become quite useful as they allow a spacecraft to fly like an airplane to maneuver to its landing site. Of course, they will eventually have to slow down, but at that point they do not need to produce as much lift, as they are descending to land.
GRADES 9–12
It might seem strange that an aircraft without any wings can produce enough lift to fly. As you can read in the section above, the key to this feat of magic is speed, and lots of it. It’s not too hard for most of us to understand how air flows around objects at low and moderate speeds; we can think of a stiff breeze blowing things around, or of driving in a car with the windows down, or any number of real-world examples. Yet at higher speeds, air starts to behave in very strange and counterintuitive ways. At low speeds, we can treat air as though it is incompressible: it flows much like water, and if it encounters an obstruction, the individual air molecules will move out of the way to go around it. But at speeds approaching the speed of sound (343 m/s or 767 mph at sea level), air starts to behave in a compressible fashion: molecules can’t move out of the way quickly enough, so they start to pile up and absorb energy. When an object is placed in a fast-moving airflow, the air starts to form waves in front of it and a rarefied region behind it, much like the bow wave in front of and the wake behind a boat. At even higher speeds, air becomes compressed and hot, and eventually starts to break apart at the molecular level.
The physics of high-speed airflows is very complicated, but amazingly, a lot of the basic trends can be captured with just two numbers: the Mach number and the Reynolds number (named after famous Austrian and British scientists Ernst Mach and Osborne Reynolds, respectively). These two numbers are non-dimensional parameters—that is, they have no units. Whether you calculate them using SI/metric or Imperial/English units, their values will be the same. Since they have no units, non-dimensional parameters like the Mach and Reynolds numbers make it possible to compare different airflow's in different circumstances directly. They allow engineers and scientists to reduce a complicated problem to a simpler set of values.
Of these two parameters, the Mach number is probably easier to understand. It is simply the speed of an airflow “V” divided by the speed of sound “a”:
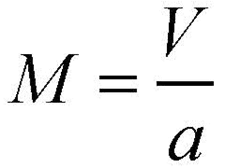
As mentioned above, the speed of sound is an important speed because it essentially marks where air starts to behave in a compressible fashion. Sound travels at different speeds based on the local temperature, but no matter what its specific speed, travel near, at, or above that speed is a guarantee that compressibility effects will be important. Here are a few examples of Mach numbers for different vehicles to give you an idea of what different Mach numbers mean:
A car at highway speed: Mach 0.09
Airliner: Mach 0.70
Speed of sound: Mach 1.00
Fighter jet: Mach 1.82
X-15 (fastest piloted aircraft): Mach 6.74
Space Shuttle: Mach 25
The other useful parameter we use to characterize airflows is the Reynolds number. This one is a bit more abstract: it is the ratio of viscous to inertialforces. In other words, it describes how much fluid friction (caused by the viscosity, or thickness, of a fluid) affects the airflow in comparison to the kinetic energy of the moving air molecules. A low Reynolds number means that the viscous friction is significant and the flow is slow and smooth; a high Reynolds number means that the friction force is insignificant because the air molecules are moving so quickly. (Even at large Reynolds numbers, the viscosity can have important effects on the flow, but the viscous forces themselves are not important.) The definition for Reynolds number is:
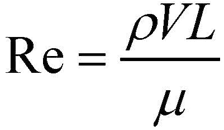
where “p” is the density, “V” is the flow velocity, “L” is a length (say, the length of an airplane’s wing), and “μ” is the (dynamic) viscosity. The Reynolds number provides insight into how smoothly air is flowing over a surface—it can relate everything from a child blowing into a pinwheel to a supersonic fighter jet.
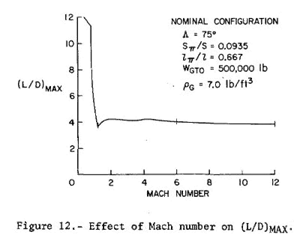
Together, the Reynolds and Mach numbers can help to describe some of the strange capabilities of high-speed aircraft such as lifting bodies. Lifting bodies are designed to fly with no wings at all. Although they are much less aerodynamically efficient than winged aircraft (as you might expect), they can nonetheless operate over a wide range of flight conditions (i.e. a wide range of Mach and Reynolds numbers) without the need to design complex wing structures that can withstand the forces of high-speed flight. They can do this because at high Mach numbers (where compressibility effects are significant) and high Reynolds numbers (where viscous/frictional effects are less significant), their unique shape allows them to consistently produce lift. For example, consider this graph (taken from a 1971 NASA study) which shows the expected glide ratio (L/D max) for a lifting body design. You can see from the figure that the glide ratio (a key measure of aircraft performance) remains relatively constant over a huge speed range—Mach 2 (about 1500 mph) to Mach 12 (about 9200 mph). This happens because at these high-Mach, high-Reynolds flight conditions, the lifting force created as the aircraft pushes its way through the air is about the same magnitude as the aerodynamic drag resulting from its blunt shape.
For a normal plane, the expected glide ratio is anywhere from 10 to 15, so a glide ratio of 4 is not that good. However, the fact that a lifting-body is able to achieve this without long, fragile wings makes it an attractive compromise—it’s easier to deal with this inefficiency than to build wings capable of withstanding the forces of high-speed flight.
Sixty Years Ago in the Space Race:
September 7, 1958: The British launched their first large-scale liquid-fueled rocket, the Black Knight, from the Woomera Test Range in Australia; it reached an altitude of 300 miles.