Aerospace Micro-Lesson #60
In This Section
Polyominoes
Most people have played a game of dominoes at some point in their lives. You can trust mathematicians to take an everyday concept and extend it in directions that most people have not thought about. This lesson explores a couple of the extensions of the concept of a domino.
Next Generation Science Standards (NGSS):
- Discipline: Engineering, Technology, and Applications of Science
- Crosscutting Concept: Patterns
- Science & Engineering Practice: Constructing explanations and designing solutions
Common Core State Standards (CCSS): Math: Geometry
- Standard for Mathematical Practice: Make sense of problems and persevere in solving them
GRADES K–2
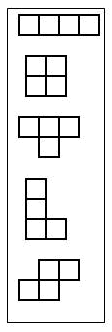 CCSS: Geometry:
Partition a rectangle into rows and columns of same-size squares and count to find the total number of them.
CCSS: Geometry:
Partition a rectangle into rows and columns of same-size squares and count to find the total number of them.
A domino is made of two squares attached along one of their sides. What happens if you attach a third square? You get a tromino (also called a “triomino,” but that term can be confused with the game of that name that involves triangles). If you attach a fourth square, you get a tetromino and a fifth square gives you apentomino.
There is only one kind of domino: it is two squares attached to each other. There are two kinds of tromino, though: you can attach the third square to the short end of the domino or on the long side of the domino. (The rules for making a polyomino dictate that the third square needs to be attached to one of the first two squares, so there is effectively only one way to attach the third square to the long side.) How many kinds of tetromino are there? (Five if you are allowed to flip them over, which is called “free polyominoes” and is conventional, or seven if you are not allowed to flip them over, which is called “one-sided polyominoes,” but I suggest you allow the kids to figure this out. Based on their shapes, they are called the “I,” “square,” “T,” “L,” and “N” tetromino.) How about pentominoes? (Twelve free or eighteen one-sided.) The number of squares, or cells, in a polyomino is called its order.
Polyominoes are something of a staple in recreational mathematics. Most people in the United States are familiar with tetrominoes from the computer game “Tetris.” Polyominoes also form the basis of many different puzzles: which polyominoes can you tile a plane with, which polyominoes can you fill a rectangle with, can you form all of the polyominoes of any given order into a rectangle, and so on. Proving that you cannot fill a 3x3 square with dominoes is trivial: the square has nine cells, each domino has two cells, and you cannot add up twos to get nine. Similarly, you cannot fill a 4x4 squares with trominoes. But how about filling up a 4x4 square with four copies of one kind of tetromino? It turns out that you can do this with every one except the “N.”
You can also use polyominoes to demonstrate different forms of symmetry. The “I” tetromino has two lines of symmetry; the square tetromino has four; the “T” tetromino has one. The “I” and “N”
tetrominoes have twofold rotational symmetry; the square tetromino has fourfold rotational symmetry. The “L” tetromino is completely asymmetric.
GRADES 3–5
 Beyond extending the idea of dominoes to multiple squares to make polyominoes, one can
extend the idea to three dimensions to get polycubes. A polycubeis a set of cubes connected at their faces. A dicube looks a lot
like a domino made with cubes; similarly, a tricubeis simply a three-dimensional version of the tromino described in the K-2 lesson. There is one kind of dicube and there are two kinds of tricube, just like the domino and tromino.
Beyond extending the idea of dominoes to multiple squares to make polyominoes, one can
extend the idea to three dimensions to get polycubes. A polycubeis a set of cubes connected at their faces. A dicube looks a lot
like a domino made with cubes; similarly, a tricubeis simply a three-dimensional version of the tromino described in the K-2 lesson. There is one kind of dicube and there are two kinds of tricube, just like the domino and tromino.
Where polycubes start to get interesting is with tetracubes. There are eight types of tetracube. Two of them are mirror images of each other; unlike polyominoes, it is not possible (in our three-dimensional universe) to “flip over” an object into its mirror image. All the puzzles involving polyominoes extend themselves to polycubes, although they are probably too advanced for students in elementary school.
One puzzle which is probably not too advanced for students in this age group is the Soma cube. The Soma cube is a puzzle in which a 3x3x3 cube is dissected into seven different pieces, each of them a polycube. One piece is the “L” tricube; the other six pieces are all the tetracubes except the “I” and the square. There are 240 distinct ways to assemble the seven pieces into a 3x3x3 cube; the pieces can also be assembled in many different ways to form many different shapes. In the latter case, the limiting factor is the person’s imagination. Soma cubes are commercially available from several different sources.
As the order of the polycube increases, things get very complicated very quickly. There are 29 different pentacubes (including six pairs of mirror images), 166 different hexacubes (including 54 mirrored pairs), and 1023 different heptacubes (including 416 mirrored pairs). Sets of pentacubes are also commercially available; at least one company also sells hexacubes.
You can use polycubes to introduce students to some basic ideas and language of three-dimensional geometry. The polycube itself is a three-dimensional polyhedron (a solid whose surfaces are all polygons, plural polyhedra); its
two-dimensional surfaces are its faces. The one-dimensional lines where two faces meet are edges; the zero-dimensional points where two or more edges meet are vertices(singular vertex). Polycubes also
provide excellent examples to illustrate convex and nonconvex solids. You may also want to point out Euler’s Polyhedron Formula, which states that for convex polyhedral the number of faces, plus the number of vertices,
minus the number of edges, equals two. The formula also holds for nonconvex polyhedra (like most polycubes) whose faces do not
intersect each other and which do not
contain any “holes” like a donut.
GRADES 6–8
Another way to extend the concept of dominoes is to change the shapes that are used as a basis for the dominoes. A domino is made up of two squares connected at an edge. A diamond is made up of two equilateral triangles connected at an edge; a polyhex is made up multiple regular hexagons connected at edges. There are many other shapes, not all of them regular, that one can use as the basis for a polyform.
Henri Picciotto has a web page with many activities involving polyominoes.
 Polyominoes themselves, starting around the order-five pentominoes, lend themselves to puzzles about packing rectangles. One can make a set of
pentominoes from card stock rather easily;
hexominoesare more work but not any more difficult conceptually. What shapes of rectangle can one pack with all of the different pentominoes? Because there are
twelve of them and each one contains five squares, the sides of the rectangles must be factors of sixty in length. One can pack rectangles of size
3 x 20,
4 x 15,
5 x 12, and
6 x 10 with pentominoes. One would think from factoring the number of cells that one could pack rectangles of dimension 3 x 70, 5 x 42, 6 x
35, 7 x 30, 10 x 21, and 14 x 15,
but this is not the case. One can, however,
assemble the hexominoes into a variety of different (mostly regular) shapes. It is very easy to prove that all the heptominoes cannot be used to pack
a rectangle; one of the heptominoes has a hole in it, leaving a blank square which no other heptomino can fill. The same is true for any higher-order polyomino.
Polyominoes themselves, starting around the order-five pentominoes, lend themselves to puzzles about packing rectangles. One can make a set of
pentominoes from card stock rather easily;
hexominoesare more work but not any more difficult conceptually. What shapes of rectangle can one pack with all of the different pentominoes? Because there are
twelve of them and each one contains five squares, the sides of the rectangles must be factors of sixty in length. One can pack rectangles of size
3 x 20,
4 x 15,
5 x 12, and
6 x 10 with pentominoes. One would think from factoring the number of cells that one could pack rectangles of dimension 3 x 70, 5 x 42, 6 x
35, 7 x 30, 10 x 21, and 14 x 15,
but this is not the case. One can, however,
assemble the hexominoes into a variety of different (mostly regular) shapes. It is very easy to prove that all the heptominoes cannot be used to pack
a rectangle; one of the heptominoes has a hole in it, leaving a blank square which no other heptomino can fill. The same is true for any higher-order polyomino.
The three-dimensional extension of packing polyominoes into a rectangle is packing polycubes into a rectangular parallelepiped. The eight tetracubes can be packed fairly easily into a cuboid with dimensions 2×4×4; note that the volume of the cuboid (2×4×4=32) must equal the number of small cubes found in all the tetracubes (4 cubes per tetracube × 8 tetracubes = 32).
Because 29 (the number of pentacubes) and 5 (the number of small cubes in a single pentacube) are both prime numbers, it is mathematically impossible to assemble them into any sort of solid rectangular shape. It is possible to assemble all the pentacubes into an “empty box” with a solid bottom and solid walls, though. If you want to create a box of size L by M by Ncubes, with N being the dimension from bottom to top, the hole in the box will be of size L–2 by M–2 by N–1. The number of cubes in the box will be given by the formula:
L x M x N - (L - 2)x(M - 2) x (N - 1)
Expanding this and setting the result equal to the number of cubes in the entire set of 29 pentacubes gives the formula:LM + 2 (L + M - 2) (N - 1) = 29 x 5 = 145
A little searching gives possible box sizes of 3×3×18, 7×7×5, 7×15×2, and 9×9×3.
The 166 hexacubes contain a total of 166×6=996 small cubes. The prime factors of 996 are 2, 2, 3, and 83. Thus a rectangular parallelepiped made by packing all the hexacubes must have dimensions of 2×3×166, 2×6×83,
or 3×4×83. I have not tried creating such a shape myself; nor have I seen whether anybody else has done it.
It is, however, possible to assemble them all into a 10×10×10 cube with four unit cubes left empty.
GRADES 9–12
CCSS: Geometry: Apply geometric methods to solve design problems.
 Prof. Kenneth Deffeyes, late of Princeton University, invented a neat little game in the mid-1980s that he called “Adlai.” It involved five or six different polycube pieces that were assembled into a 3x3x3 cube. Most or all of
the pieces were asymmetric—the term “enantiomorph” was used in connection with the game—and the game kit involved a left-handed and right-handed version of each asymmetric piece. In a game, the players would begin by
each taking one of each pair of pieces. After they had taken all of the pieces, they were to assemble their pieces into a cube; the first person successfully to assemble his pieces was the winner and would say “Adlai” when he finished.
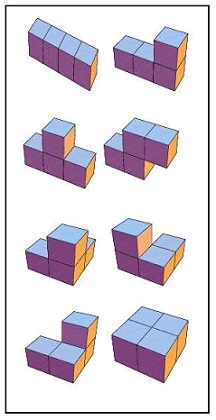
Unfortunately the exact shapes of the pieces have been lost to the mists of time. While your writer remembers there being six asymmetric pieces, the numbers of cubes in the required pieces do not add up to 27. There may have been two copies
of a symmetric tricube (the “L” one), the asymmetric tetracubes, and the left- and right-handed versions of four of the six asymmetric pentacubes. Your writer remembers being able to look at each of the pieces and distinguish rather
easily a “clockwise” and “counterclockwise” twist to them; if a player selected all “clockwise” pieces in the first part of the game there was no way to assemble them into a cube. While it is not guaranteed,
it is possible that the four pentacubes were the ones pictured here (as well as their mirror images).
Prof. Kenneth Deffeyes, late of Princeton University, invented a neat little game in the mid-1980s that he called “Adlai.” It involved five or six different polycube pieces that were assembled into a 3x3x3 cube. Most or all of
the pieces were asymmetric—the term “enantiomorph” was used in connection with the game—and the game kit involved a left-handed and right-handed version of each asymmetric piece. In a game, the players would begin by
each taking one of each pair of pieces. After they had taken all of the pieces, they were to assemble their pieces into a cube; the first person successfully to assemble his pieces was the winner and would say “Adlai” when he finished.
Unfortunately the exact shapes of the pieces have been lost to the mists of time. While your writer remembers there being six asymmetric pieces, the numbers of cubes in the required pieces do not add up to 27. There may have been two copies
of a symmetric tricube (the “L” one), the asymmetric tetracubes, and the left- and right-handed versions of four of the six asymmetric pentacubes. Your writer remembers being able to look at each of the pieces and distinguish rather
easily a “clockwise” and “counterclockwise” twist to them; if a player selected all “clockwise” pieces in the first part of the game there was no way to assemble them into a cube. While it is not guaranteed,
it is possible that the four pentacubes were the ones pictured here (as well as their mirror images).
When one is extending planar figures into higher dimensions, there is no reason to stop with three-dimensional objects. A four-dimensional polycube—which is obscure enough that it does not even have a name, although “polytesseract” would be appropriate—is the next step. Visualizing a single tesseract is difficult enough; visualizing a polytesseract is harder. One does not need to be able to visualize something in order to work with it, though. For example, it is fairly easy to prove that there are as many order-four polytesseracts as there are tetracubes; the argument is similar to the one proving that there are as many tricubes as there are trominoes. (Depending on the definition of an order-four tesseract, there may be one fewer; in four dimensions one can “turn over” one asymmetric tetracube into its mirror image.) Beyond that, it is not clear that there has been any research at all into polytesseracts—the number of polytesseracts of each order, whether some set of them can fill a four-dimensional “box,” and so on. It has been shown that there are 1,390 distinct ways to assemble the eight tetracubes into a three-dimensional box of size 2 x 4 x 4; it is not known whether the same shapes, extended into four dimensions, can be assembled into a box of size 2 x 2 x 2 x 4.
Suggested Activity: If some of your students are handy with woodworking, they can make a few sets of “Adlai” pieces. A set of suggested shapes is given in the figure on the previous page. If you do not want to go the route of making pieces from scratch, you can glue together children’s alphabet blocks.
Sixty Years Ago in the Space Race:
