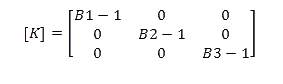Guidelines for Mathematics in AIAA Journals

Symbology

Keep equations simple and avoid unusual characters or symbols. Use MathType or some other interactive equation-editing software to create your equations so that they can be edited during production, if necessary. Do not convert your equations into images. To expedite the editorial and composition process, authors are asked to comply with the following:

1. Avoid using under-barred symbols.
2. Avoid using multiple dot accents (in excess of two).
3. In the case of barred variables, it is conventional to use a bar accent (ā) for a single variable and a continuous rule (abc) for several variables.
4. Punctuation may be used to separate mathematical expressions displayed on the same line, but no punctuation is used at the end of each line (including periods at the end of an equation).

Subscripts and Superscripts

Avoid symbols with multiple layers of subscripts or superscripts. It is better to use several symbols in a subscript rather than several layers. For example, use X_A1 rather than X_A1 . The same applies to superscripts. In any case, more than a two-layered sub- or superscript should not be used.

Vectors

When there is a distinction to be made between vector and scalar quantities, use boldface type for the vector quantities rather than bars or arrows above the symbol. Boldface type is available for regular, italic, and Greek typefaces.

Italic vs Regular Characters

Use italic (slanted) type for all variables and constants, with some exceptions. Set in regular (upright) type: sin, cos, tan,..., and all similar trigonometric and hyperbolic functions: log for base 10 logarithms; qualities such as min, max, opt,..., etc.; and “d” for derivative. Symbols for descriptive terms are set in regular type when they are subscripts or superscripts. Acronyms used in mathematical expressions also are regular type. The “ln” for natural logarithm will be set in script: (Ln)

Note: When exponential notation is used, the form e_xyz is preferred. Use the form exp[x2 + (y – 1) – 3 + z] when the exponents of the natural base are unusually long or complicated, i.e., containing fractions, integrals, or sigma summations.

Derivatives

A derivative of a quantity can be indicated by an over dot or a prime. The X' is preferred and is available up to the fourth derivative. Single/double over dots are available.

Accents

The seven common mathematical accents can be placed above any italic, regular, or Greek letter automatically. Accents should not be stacked one over the other. These accents also can be used over German and script letters, but this application is not recommended.

Fractions

To keep equations as compact as possible, small fractions are usually “broken down” in solidus (/) form. This is especially true if the equation does not contain integrals or summations. However, do not mix built-up fractions and fractions with a solidus. Fractions with long numerators or denominators (five or more characters) should be displayed and left as built-up fractions for readability.

Radicals

Radical signs of arbitrary length are available for use over variables (with or without a superscript) and simple fractions. When a radical is needed over an accented or barred variable, a variable with layered superscripts, or a complex fraction (where the numerator or denominator contains a fraction, integral, or sigma summation), the exponential notation ( )^1/2 should be used.

Multiple-Line Equations

Long equations are broken apart and continued for several lines. The point at which such equations should be broken is best determined by the author so that the breaks fit conveniently with the concept being expressed. A rule of thumb on the amount that will fit on one line in the published journal PDF format is 40 symbols that take horizontal space, counting all regular characters, sub- and superscripts, parentheses, plus and minus signs, etc.

Example:

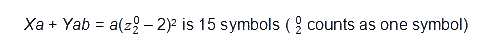
Integral and summation signs each count as three symbols. Authors should format individual lines of equations to be no more than 40 symbols wide to ensure that they ”break” logically on the printed page. AIAA style requires that the second line of a “broken” equation start with the connective math sign; i.e.,

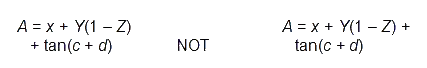
Number each equation consecutively in parentheses to the right of the equation or to the right of the last line of a “broken” equation. Groups of equations that the author wants to identify with one equation number preferably should be individually numbered (1a), (1b), (1c), etc. The exception is a matrix, where the equation number is on the right of the midpoint of the matrix.

Matrices

Center matrices vertically about the “main line” or midpoint of each matrix, and separate each row in a matrix with a blank line.